题目内容
17. 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于1:3.
如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于1:3.
分析 根据三角形的中位线平行于第三边并且等于第三边的一半,可以求出DE=$\frac{1}{2}$BC,又点M是DE的中点,可以求出DM:BC的值,也就等于MN:NC的值,从而可以得到MN:MC的比值,也就是点N到DE的距离与点C到DE的距离之比,又DM=ME,所以S△DMN:S△CEM=MN:MC.
解答  解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∵M是DE的中点,
∴DM=ME=$\frac{1}{2}$BC,
∴$\frac{MN}{NC}$=$\frac{DM}{BC}$=$\frac{1}{4}$,
∴$\frac{MN}{MC}$=$\frac{NF}{CG}$=$\frac{1}{3}$,
即:点N到DE的距离与点C到DE的距离之比为$\frac{1}{3}$,
∵DM=ME,
∴S△DMN:S△CEM=1:3.
故答案为:1:3.
点评 此题考查了相似三角形的判定与性质,根据三角形的中位线定理,以及平行线分线段成比例定理,求出等边上的高的比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.如果2x=3y(x、y均不为0),那么下列各式中正确的是( )
| A. | $\frac{x}{y}$=$\frac{2}{3}$ | B. | $\frac{x}{x-y}$=3 | C. | $\frac{x+y}{y}$=$\frac{5}{3}$ | D. | $\frac{x}{x+y}$=$\frac{2}{5}$ |
7.下列各组中的四条线段成比例的是( )
| A. | 1cm、2cm、20cm、30cm | B. | 1cm、2cm、3cm、4cm | ||
| C. | 5cm、10cm、10cm、20cm | D. | 4cm、2cm、1cm、3cm |
 如图,一只蚂蚁从长、宽都是2,高是5的长方体纸盒的A点沿纸盒面爬到B点,那么它所行的最短路线的长是$\sqrt{41}$.
如图,一只蚂蚁从长、宽都是2,高是5的长方体纸盒的A点沿纸盒面爬到B点,那么它所行的最短路线的长是$\sqrt{41}$. 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.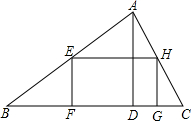 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).
如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).