题目内容
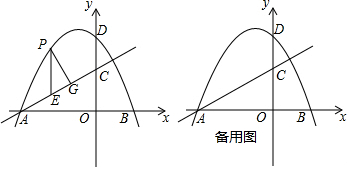
8.已知:如图1,菱形ABCD的边长为4cm,P、Q分别是AB、BC两边上的动点,P、Q分别从A、B两点同时出发,均以1cm/s的速度沿AB、BC向点B和点C匀速运动,当点P到达点B时停止运动,点Q也随之停止运动.设运动时间为t(s),点P到AD的距离与点Q到CD的距离差的绝对值为y(cm),且y与t的函数图象如图2所示.
(1)∠A的度数为60°,M点的坐标所表示的实际意义是点P到AD的距离和点Q到CD的距离相等;
(2)求证:PD=QD;
(3)当y=$\frac{\sqrt{3}}{2}$时,求t的值.
分析 (1)先由图2判断出菱形ABCD的高为2$\sqrt{3}$,然后利用锐角三角函数即可得出结论;
(2)先判断出△BCD是等边三角形,进而判断出△BDQ≌△ADP,即可得出结论;
(3)构造出直角三角形,利用三角形函数得出PE和PF,进而得出y=$\sqrt{3}$|t-2|,再将y=$\frac{\sqrt{3}}{2}$代入即可得出结论.
解答 解:(1)如图1,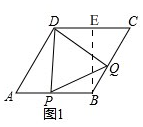
过B作BE⊥CD于E,
由图2知,
运动时间t=0时,点P到AD的距离为0,点Q到CD的距离是菱形的高为2$\sqrt{3}$,
即:BE=2$\sqrt{3}$,
在Rt△BCE中,BC=4,BE=2$\sqrt{3}$,
∴sin∠C=$\frac{BE}{BC}$=$\frac{\sqrt{3}}{2}$,
∴∠A=∠C=60°,
由图2知,点M在x轴上,
∴M点的坐标所表示的意义是点P到AD的距离和点Q到CD的距离相等;
故答案为60°,点P到AD的距离和点Q到CD的距离相等;
(2)如图3,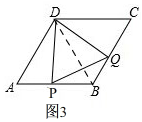
连接BD,由(1)知,∠C=60°,
∵BC=CD,
∴△BCD是等边三角形,
∴DB=BC=AD,∠DBQ=60°=∠A,
由运动知,AP=BQ,
在△BDQ和△ADP中,$\left\{\begin{array}{l}{BD=AD}\\{∠DBQ=∠A}\\{BQ=AP}\end{array}\right.$,
∴△BDQ≌△ADP,
∴QD=PD;
(3)如图4,
过点P作PE⊥AD,过点Q作QF⊥CD,
由运动知,AP=AQ=t,(0≤t≤4)
∴CQ=4-t,
在Rt△APE中,∠A=60°,AP=t,
∴PE=AP•sin∠A=$\frac{\sqrt{3}}{2}$t,
同理:FQ=$\frac{\sqrt{3}}{2}$(4-t),
∴y=|$\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{2}$(4-t)|=$\frac{\sqrt{3}}{2}$|2t-4|=$\sqrt{3}$|t-2|,
∵y=$\frac{\sqrt{3}}{2}$,
∴2|t-2|=1,
∴t=$\frac{3}{2}$或t=$\frac{5}{2}$.
点评 此题是四边形综合题,主要考查了菱形的性质,锐角三角函数的意义,全等三角形的判定和性质,解(1)的关键是从图2中得出菱形的高,解(2)的关键是构造出全等三角形,解(3)的关键是建立y与t的函数关系式,是一道中等难度的中考常考题.

 如图,已知A(m,3)是一次函数y=kx+b与反函数y=$\frac{6}{x}$(x>0)的交点.
如图,已知A(m,3)是一次函数y=kx+b与反函数y=$\frac{6}{x}$(x>0)的交点.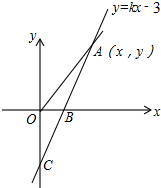 如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB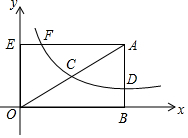 如图,矩形ABOE的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,矩形ABOE的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.