题目内容
16. 如图,已知A(m,3)是一次函数y=kx+b与反函数y=$\frac{6}{x}$(x>0)的交点.
如图,已知A(m,3)是一次函数y=kx+b与反函数y=$\frac{6}{x}$(x>0)的交点.(1)求m的值;
(2)若一次函数分别与x、y轴交于E、F两点,A为EF的中点,试求该一次函数的解析式;
(3)在y=$\frac{6}{x}$的图象上另取一点B,作BK⊥x轴于K,在(2)的条件下,在y轴上取一点C,使得FO=4CO.问:在y轴上是否存在点P,使得△PAC和△PBK的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
分析 (1)利用待定系数法求出m的值,
(2)利用中点坐标即可求出k,b的值,进而得出直线EF的解析式;
(3)设出点P的坐标,表示出三角形PAC的面积,再求出三角形PBK的面积建立方程即可得出P的坐标.
解答 解:(1)∵点A(m,3)在反比例函数y=$\frac{6}{x}$的图形上,
∴3m=6,
∴m=2,
(2)由(1)知,A(2,3),
∵点A在一次函数y=kx+b的图象上,
∴2k+b=3,
∴b=3-2k,
∴一次函数的解析式为y=kx+3-2k,
令y=0,
∴x=$\frac{2k-3}{k}$,
∴E($\frac{2k-3}{k}$,0),F(0,3-2k),
∵A(2,3)是EF的中点,
∴3-2k=6,
∴k=-$\frac{3}{2}$,
∴b=6,
∴一次函数额解析式为y=-$\frac{3}{2}$x+6;
(3)由(2)知,E(4,0),F(0,6),
∴OF=6,
∵FO=4OC=6,
∴OC=$\frac{3}{2}$,
∴C(0,$\frac{3}{2}$),
设P(0,t),
∴PC=|t-$\frac{3}{2}$|,
∴S△PAC=$\frac{1}{2}$PC•xA=$\frac{1}{2}$×|t-$\frac{3}{2}$|×2=|t-$\frac{3}{2}$|,
设B(n,$\frac{6}{n}$),
∴OK=n,BK=$\frac{6}{n}$,
∴S△PBK=$\frac{1}{2}$BK•OK=$\frac{1}{2}$×$\frac{6}{n}$×n=3,
∵△PAC和△PBK的面积相等,
∴|t-$\frac{3}{2}$|=3,
∴t=$\frac{9}{2}$或t=-$\frac{3}{2}$,
∴P(0,$\frac{9}{2}$)或(0,-$\frac{3}{2}$).
点评 此题是反比例函数综合题,主要考查了待定系数法,点的中点坐标,三角形的面积公式,解(2)的关键是得出点E,F的坐标,解(3)的关键是求出三角形PBK的面积是3,是一道中等难度的题目.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案| A. | 9 | B. | -3 | C. | 12 | D. | 不确定 |
| A. | $-\frac{7}{4}$ | B. | $-\frac{17}{8}$ | C. | -2 | D. | -3 |
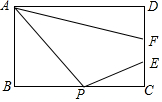 如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
 如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.
如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.

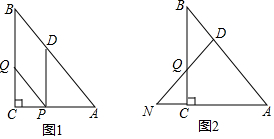 如图1,在Rt△ABC中,∠C=90°,AC=54,BC=72,动点P从点A开始沿边AC向点C以每秒3个单位长度的速度运动,动点Q从点C开使沿边CB向点B运动,过点P作PD∥BC,交AB于点D,连接PQ,点P、Q同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒(t≥0).
如图1,在Rt△ABC中,∠C=90°,AC=54,BC=72,动点P从点A开始沿边AC向点C以每秒3个单位长度的速度运动,动点Q从点C开使沿边CB向点B运动,过点P作PD∥BC,交AB于点D,连接PQ,点P、Q同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒(t≥0).