题目内容
8.某水利部门为了加强公民的节水和用水意识,合理利用水资源,采用了价格调控手段以期达到公民节约用水的目的.规定用水收费标准如下:每户每月的用水不超过10立方米时,水费按每立方米a元收费;超过10立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.小颖家今年5、6月份的用水量和水费如表所示:| 月份 | 用水量(立方米) | 收费(元) |
| 5 | 9 | 14.4 |
| 6 | 13 | 23.8 |
(1)求a,b的值;
(2)写出y与x之间的表达式;
(2)若小颖家7月份的用水量为15.5立方米,求她家7月份的水费是多少元?
分析 (1)根据不超过10立方米时,单价=总价÷数量即可求得a;超过10立方米时,比16元多出的价格,除以3,即可求得b;
(2)分x≤10和x>10两种情况,用含x的式子表示y即可;
(3)将将x=15.5代入y=2.6x-10,直接计算即可.
解答 解:(1)根据题意,当x≤10时,y=ax,
由已知,14.4=9a,解得:a=1.6,
当x>10时,y=10×1.6+b(x-10)=16+b(x-10),
由已知,23.8=16+b(13-10),得:b=2.6;
(2)y与x之间的表达式;
当x≤10时,y=1.6x,
当x>10时,y=1.6×10+2.6(x-10)=2.6x-10;
(3)将x=15.5代入y=2.6x-10,
得:y=30.3(元).
点评 本题主要考查一次函数的应用,解决此类题目时,能从题目中抽象出函数是解题的关键,此题中要主要x≤10和x>10两种情况下,函数也是不同的.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.要使等式4xy+M=(x+y)2成立,代数式M为( )
| A. | x2-y2 | B. | (x-y)2 | C. | x2+y2 | D. | (x+y)2 |
10. 如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )
如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )
 如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )
如图,△ABC内接于⊙O,若∠OAB=26°,则∠C的大小为( )| A. | 26° | B. | 52° | C. | 60° | D. | 64° |
7.已知方程组$\left\{\begin{array}{l}{ax+by=6}\\{bx+ay=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,则a,b的值分别为( )
| A. | 5,4 | B. | 4,5 | C. | -5,4 | D. | 5,-4 |
3.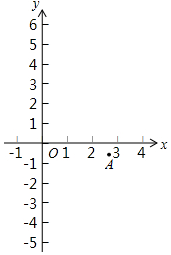 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
①m=-60;
②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
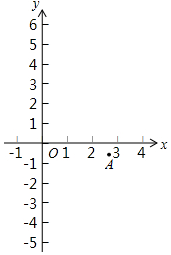 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
 如图,∠B=∠C=90°,DE平分∠ADC,AE平分∠DAB,求证:E是BC的中点.
如图,∠B=∠C=90°,DE平分∠ADC,AE平分∠DAB,求证:E是BC的中点.