题目内容
9.已知关于x的分式方程$\frac{a-x}{x+1}$=1的解小于零,求a的取值范围.分析 由于本题是关于x的分式方程,那么就可以把a当作已知数,求得x的解.再根据根于小0,分母不为0求得a的取值.
解答 解:方程两边都乘以x+1得,a-x=x+1,
解得x=$\frac{a-1}{2}$.
∵关于x的分式方程$\frac{a-x}{x+1}$=1的解小于0,
∴$\frac{a-1}{2}$<0且x+1≠0,
∴a<1且$\frac{a-1}{2}$≠-1,
∴a<1且a≠-1,
即a的取值范围为a<1且a≠-1.
点评 本题考查了分式方程的解,关于某个字母的方程,应该只把这个字母当成未知数,其余的当成已知数来解.本题还需注意分母不能为0.

练习册系列答案
相关题目
17.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
| A. | 11 | B. | 14 | C. | 19 | D. | 14或19 |
14.下列计算中正确的是( )
| A. | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B. | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C. | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D. | $\sqrt{{{({-3})}^2}}=-3$ |
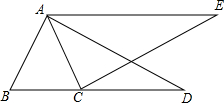 如图,在△ABC中,∠ABC=∠ACB,过A作AD⊥AB交BC的延长线于D,过C作CE⊥AC使AE=BD.求证:∠E=∠D.
如图,在△ABC中,∠ABC=∠ACB,过A作AD⊥AB交BC的延长线于D,过C作CE⊥AC使AE=BD.求证:∠E=∠D.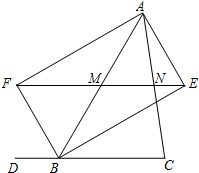 已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证: