题目内容
18.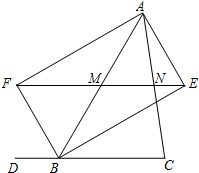 已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:(1)四边形AFBE是矩形;
(2)MN=$\frac{1}{2}$BC.
分析 (1)由BE、BE是角平分线可得∠EBF是90°,进而由条件中的两个垂直可得两个直角,可得四边形AEBF是矩形;
(2)由矩形的F质可得∠2=∠5进而利用角平分线的性质可得∠1=∠5,可得ME∥BC,进而可得N为AC中点,根据三角形中位线性质求出即可.
解答  证明:(1)∵BE、BF分别是△ABC中∠B及它的外角的平分线,
证明:(1)∵BE、BF分别是△ABC中∠B及它的外角的平分线,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵AE⊥BE,E为垂足,AF⊥BF,F为垂足,
∴∠AFB=∠AEB=90°,
∴四边形AEBF为矩形;
(2)∵四边形AEBF为矩形,
∴BM=MA=ME,
∴∠2=∠5,
∵∠2=∠1,
∴∠1=∠5,
∴ME∥BC,
∵M是AB的中点,
∴N为AC的中点,
∴MN=$\frac{1}{2}$BC.
点评 本题考查了矩形的判定与性质,三角形中位线性质,平行线的判定的应用,用到的知识点为:有3个角是直角的四边形是矩形;矩形的对角线平分且相等.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
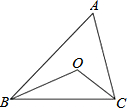 如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:
如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求: 如图,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G,若∠EFG=56°,则∠2-∠1=44°.
如图,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G,若∠EFG=56°,则∠2-∠1=44°.