题目内容
20.关于x的方程kx2+(k+2)x+$\frac{k}{4}$=0有两个不相等的实数根.(Ⅰ)求k的取值范围;
(Ⅱ)当k=4时,求方程的解.
分析 (Ⅰ)根据根的判别式建立关于k的方程,求得k的取值范围即可;
(Ⅱ)把k=4代入方程求得方程的解即可.
解答 解:(Ⅰ)∵x的方程kx2+(k+2)x+$\frac{k}{4}$=0有两个不相等的实数根,
∴k≠0,且△>0,即(k+2)2-4•k•$\frac{k}{4}$>0,解得k>-1,
∴k的取值范围为:k>-1且k≠0.
(Ⅱ)当k=4时,原方程为4x2+6x+1=0
解得:$x=\frac{{-3±\sqrt{5}}}{4}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
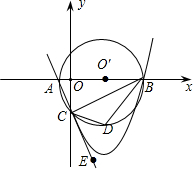 如图,已知A(-1,0),B(9,0),以AB为直径的圆P交y轴负半轴于C,连接AC,BC,
如图,已知A(-1,0),B(9,0),以AB为直径的圆P交y轴负半轴于C,连接AC,BC,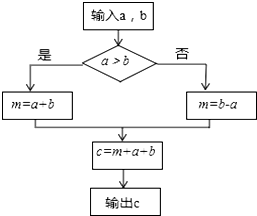 已知a、b为两个不相等的有理数,根据流程图中的程序:
已知a、b为两个不相等的有理数,根据流程图中的程序: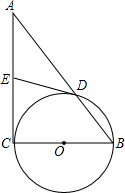 如图,在Rt△ABC中,∠ACB=90°,以BC为直径作⊙O,交AB于点D,取AC的中点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径作⊙O,交AB于点D,取AC的中点E,连接DE.