题目内容
4.如果-$\frac{5}{3}$a>-$\frac{2}{7}$a,2+c>2,试比较ac+a与-ac+a的大小.分析 根据已知条件可得到a<0,c>0,进而可得到较ac+a与-ac+a的大小.
解答 解:∵-$\frac{5}{3}$a>-$\frac{2}{7}$a,
∴$\frac{5}{3}$a<$\frac{2}{7}$a,
∴a<0,
∵2+c>2,
∴c>0,
∴ac<0,
∴ac+a-(-ac+a)=2ac<0,
即ac+a<-ac+a.
点评 本题主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
14. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
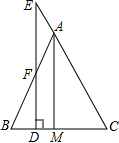 如图,在△ABC中,AB=AC,AM是BC边的中线,点E在CA的延长线上,ED∥AM交BC于D,交AB于F,求证:AE=AF.
如图,在△ABC中,AB=AC,AM是BC边的中线,点E在CA的延长线上,ED∥AM交BC于D,交AB于F,求证:AE=AF.
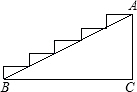 如图:在一个高6米,长10米的楼梯表面铺地毯,则该地毯的长度至少是14米.
如图:在一个高6米,长10米的楼梯表面铺地毯,则该地毯的长度至少是14米.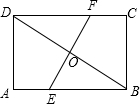 如图所示,在矩形ABCD中,EF是BD的垂直平分线,BD=40米,EF=30米,求证四边形BEDF是菱形,并求出它的面积.
如图所示,在矩形ABCD中,EF是BD的垂直平分线,BD=40米,EF=30米,求证四边形BEDF是菱形,并求出它的面积.