题目内容
15．
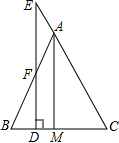如图，在△ABC中，AB=AC，AM是BC边的中线，点E在CA的延长线上，ED∥AM交BC于D，交AB于F，求证：AE=AF．
分析 根据等腰三角形的三线合一，可得AM⊥BC，AM∥ED，即可得出ED⊥BC，根据互余可得，∠E+∠C=90°，∠B+∠BFD=90°，结合对顶角相等，可得出∠E=∠EFA，即可证得；
解答 证明：∵AB=AC，M为BC边的中点，
∴AM⊥BC，∠B=∠C，
∵AM∥ED，
∴ED⊥BC，
∵∠E+∠C=90°，∠B+∠BFD=90°，
∠B=∠C，
∴∠E=∠BFD，
又∵∠BFD=∠AFE，
∴∠E=∠AFE，
∴AE=AF．
点评 本题主要考查了等腰三角形的性质，互余的定义，对顶角的性质，利用等腰三角形的三线合一是解答此题的关键．
练习册系列答案
相关题目
5．
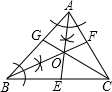如图，AE于BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法不正确的是（ ）
如图，AE于BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法不正确的是（ ）| A． | AE、BF是△ABC的内角平分线 | B． | 点O到△ABC三边的距离相等 | ||
| C． | CG也是△ABC的一条内角平分线 | D． | AO=BO=CO |
6．
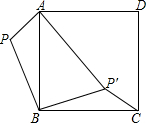如图，已知P为正方形ABCD外的一点，PA=1，PB=2，将△ABP绕点B顺时针旋转90°，使点P旋转至点P′，且AP′=3，则∠BP′C的度数为 （ ）
如图，已知P为正方形ABCD外的一点，PA=1，PB=2，将△ABP绕点B顺时针旋转90°，使点P旋转至点P′，且AP′=3，则∠BP′C的度数为 （ ）| A． | 105° | B． | 112.5° | C． | 120° | D． | 135° |
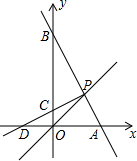如图，在平面直角坐标系中，直线y=x与直线y=-2x+3交于点P，直线y=-2x+3与x轴交于点A，与y轴交于B．
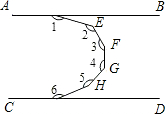如图，两直线AB，CD平行，求∠1+∠2+∠3+∠4+∠5+∠6的值．