题目内容
6.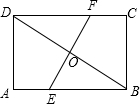 如图所示,在矩形ABCD中,EF是BD的垂直平分线,BD=40米,EF=30米,求证四边形BEDF是菱形,并求出它的面积.
如图所示,在矩形ABCD中,EF是BD的垂直平分线,BD=40米,EF=30米,求证四边形BEDF是菱形,并求出它的面积.
分析 连接DE、BF,因为四边形ABCD是矩形,所以AB∥CD,进而求证DF=BE,再求证FD=FB,即可判定四边形BFDE是菱形;根据菱形面积计算公式即可计算菱形BFDE的面积.
解答 (1)证明:如图,连接DE、BF,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ODF=∠OBE,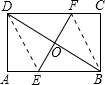
由EF垂直平分BD,
得OD=OB,∠DOF=∠BOE=90°,
∴△DOF是△BOE成旋转对称,
故DF=BE,
∴四边形BEDF是平行四边形,
又∵EF是BD的垂直平分线,
∴FD=FB,
∴四边形BFDE是菱形;
(2)解:∵四边形BFDE是菱形;
∴S菱形BFDE=$\frac{1}{2}$EF•BD=$\frac{1}{2}$×30×40=600(米2).
答:四边形BFDE的面积为600(米2).
点评 本题考查了菱形的判定,矩形对边相等且平行的性质,垂直平分线的性质,本题中求证DF=BE是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
18.为了应对期末考试,老师布置了15道选择题作业,批阅后得到如下统计表,根据表中数据可知,由45名学生答对题数组成的样本的中位数是14.
| 答对题数(道) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 18 | 16 | 7 |
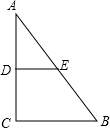 如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.
如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.