题目内容
14. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 由于点B与D关于AC对称,所以连接BD,与AC的交点即为F点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,从而得出结果.
解答 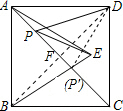 解:连接BD,与AC交于点F.
解:连接BD,与AC交于点F.
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,
∴AB=2$\sqrt{3}$.
又∵△ABE是等边三角形,
∴BE=AB=2$\sqrt{3}$.
故所求最小值为2$\sqrt{3}$.
故选B.
点评 此题主要考查了轴对称--最短路线问题,难点主要是确定点P的位置.注意充分运用正方形的性质:正方形的对角线互相垂直平分.再根据对称性确定点P的位置即可.要灵活运用对称性解决此类问题.

练习册系列答案
相关题目
5.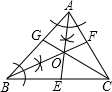 如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
 如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )| A. | AE、BF是△ABC的内角平分线 | B. | 点O到△ABC三边的距离相等 | ||
| C. | CG也是△ABC的一条内角平分线 | D. | AO=BO=CO |
19.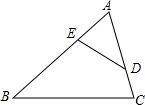 如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
 如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
6.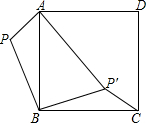 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )| A. | 105° | B. | 112.5° | C. | 120° | D. | 135° |
 甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )
甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )
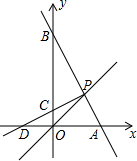 如图,在平面直角坐标系中,直线y=x与直线y=-2x+3交于点P,直线y=-2x+3与x轴交于点A,与y轴交于B.
如图,在平面直角坐标系中,直线y=x与直线y=-2x+3交于点P,直线y=-2x+3与x轴交于点A,与y轴交于B.