题目内容
9.解方程:(1)2(x+2)2-8=0;
(2)x(x-3)=3-x;
(3)$\sqrt{3}$x2=6x-$\sqrt{3}$;
(4)(x+3)2+3(x+3)-4=0.
分析 (1)方程整理后,利用平方根定义开方即可求出解;
(2)方程整理后,利用因式分解法求出解即可;
(3)方程整理后,利用公式法求出解即可;
(4)方程利用因式分解法求出解即可.
解答 解:(1)方程整理得:(x+2)2=4,
开方得:x+2=2或x+2=-2,
解得:x1=0,x2=-4;
(2)方程整理得:x(x-3)+(x-3)=0,
分解因式得:(x-3)(x+1)=0,
解得:x1=3,x2=-1;
(3)方程整理得:$\sqrt{3}$x2-6x+$\sqrt{3}$=0,
这里a=$\sqrt{3}$,b=-6,c=$\sqrt{3}$,
∵△=36-12=24,
∴x=$\frac{6±2\sqrt{6}}{2\sqrt{3}}$=$\sqrt{3}$±$\sqrt{2}$;
(4)(x+3)2+3(x+3)-4=0,
分解因式得:(x+3-1)(x+3+4)=0,
解得:x1=-2,x2=-7.
点评 此题考查了解一元二次方程-因式分解法,公式法,以及直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
19.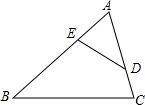 如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
 如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
1.用m个正方形和n个正八边形铺设地面,则m、n满足的条件是( )
| A. | 2m+3n=8 | B. | 3m+2n=8 | C. | m+n=4 | D. | m+2n=6 |
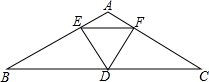 如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.
如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.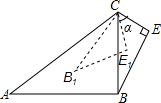 如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.
如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.