题目内容
5. 在下列坐标系中画出y=x的图象.
在下列坐标系中画出y=x的图象.(1)若点A是该函数图象第一象限上的点,且OA=2$\sqrt{2}$,求点A的坐标;
(2)在x轴上求作一点P,使△AOP是等腰三角形,请直接写出点P的坐标.
分析 (1)设出点A的坐标,利用勾股定理即可解答;
(2)分三种情况讨论:当OD=AD时、当OA=OD时、当AO=AD时,进行解答.
解答 解:如图,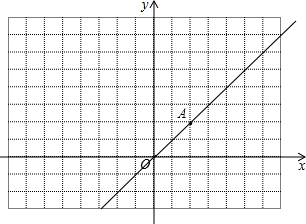
(1)设点A的坐标是(x,y),
∵点A是该函数图象y=x第一象限上的点,
∴y=x,
∴${x}^{2}+{y}^{2}=(2\sqrt{2})^{2}$,
∴x=2,y=2,
∴点A的坐标为(2,2).
(2)当OD=AD时,点D的坐标为(2,0);
当OA=OD时,点D的坐标为(2$\sqrt{2}$,0)或(-2$\sqrt{2}$,0);
当AO=AD时,点D的坐标为(4,0).
点评 本题考查了等腰三角形的判定,解决本题的关键是在判定等腰三角形时进行分类讨论.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
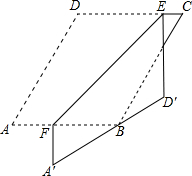 如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.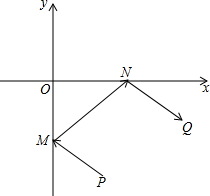 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.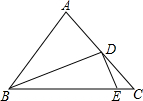 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )