题目内容
10.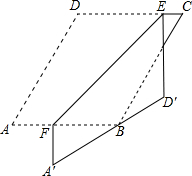 如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
分析 首先延长DC与A′D′的延长线交于点H,由四边形ABCD是菱形与折叠的性质,易求得△BCH是等腰三角形,△D′FH是含30°角的直角三角形,然后设DE=x,利用正切函数的知识,即可求得答案.
解答 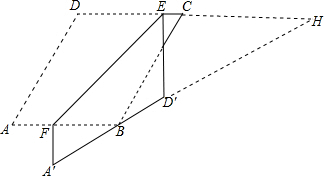 解:延长DC,交A′D′的延长线于H,
解:延长DC,交A′D′的延长线于H,
∵四边形ABCD是平行四边形,∠A=60°,
∴∠D=120°,∠DCB=∠A=60°,
由翻转变换的性质可知,∠ED′B=120°,
∴∠ED′H=60°,又D′E⊥CD,
∴∠H=30°,
∴∠CBH=30°,
∴CB=CH,
设DE=x,则DC=x+1,D′E=x,
∵AD-AB=1,
∴BC=x+1+1=x+2,
∴CH=x+2,
∴EH=x+3,
∵tan∠H=$\frac{ED′}{EH}$,
∴$\frac{x}{x+3}$=$\frac{\sqrt{3}}{3}$,
解得,x=$\frac{3\sqrt{3}+3}{2}$,
∴AB=DC=$\frac{3\sqrt{3}+5}{2}$,
故答案为:$\frac{3\sqrt{3}+5}{2}$.
点评 本题考查了折叠的性质、菱形的性质、等腰三角形的判定与性质以及直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意折叠中的对应关系,注意数形结合思想的应用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
20.下列等式成立的是( )
| A. | $\frac{2}{2x+y}=\frac{1}{x+y}$ | B. | (-x-1)(1-x)=1-x2 | C. | $\frac{x}{-x+y}=-\frac{x}{x+y}$ | D. | (-x-1)2=x2+2x+1 |
 如图,已知∠BOD=110°,求∠A+∠B+∠C+∠D.
如图,已知∠BOD=110°,求∠A+∠B+∠C+∠D.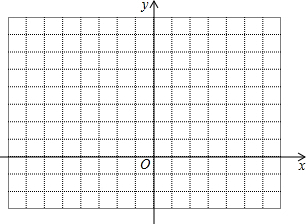 在下列坐标系中画出y=x的图象.
在下列坐标系中画出y=x的图象.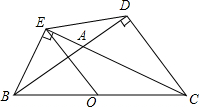 如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE.
如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE. 如图,已知正方形ABCD的边长为$\sqrt{5}$,点E,F,G,H分别在正方形的四条边上,且AE=DF=CG=BH,则四边形EFGH的形状为正方形,它的面积的最小值为$\frac{5}{2}$.
如图,已知正方形ABCD的边长为$\sqrt{5}$,点E,F,G,H分别在正方形的四条边上,且AE=DF=CG=BH,则四边形EFGH的形状为正方形,它的面积的最小值为$\frac{5}{2}$.