题目内容
17.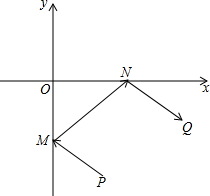 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.(1)请你作出最短路线并简要说明作法;
(2)求最短路线中草地边的牧马点M和河边饮水点N的坐标;
(3)求这个最短路线的长度.
分析 (1)如图,作点P关于y轴的对称点E,点Q关于x轴的对称点F,连接EF分别与x、y轴交于点N、M,此时PM+MN+NQ最小.
(2)根据E、F两点坐标求出直线EF的解析式,再分别令x=0,y=0求出点M、N的坐标.
(3)延长EP、FQ交于点H,在RT△EFH中利用勾股定理求出EF即可.
解答 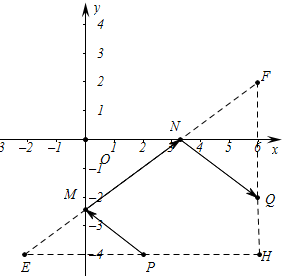 解:(1)如图,作点P关于y轴的对称点E,点Q关于x轴的对称点F,连接EF分别与x、y轴交于点N、M.
解:(1)如图,作点P关于y轴的对称点E,点Q关于x轴的对称点F,连接EF分别与x、y轴交于点N、M.
∵PM=EM,NF=NQ,
∴PM+MN+NQEM+MN+NF=EF,
∴此时PM+MN+NQ最小(两点之间线段最短).
(2)∵点E坐标(-2,-4),点F坐标(6,2),
∴最小EF的解析式为y=$\frac{3}{4}$x-$\frac{5}{2}$,
∴点M坐标(0,-$\frac{5}{2}$),点N坐标($\frac{10}{3}$,0).
(3)延长EP、FQ交于点H,
由(1)可知PM+MN+NQ的最小值=EF=$\sqrt{E{H}^{2}+F{H}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10.
点评 本题考查最短问题、坐标与图形、待定系数法求一次函数的解析式、勾股定理等知识,利用对称根据两点之间线段最短找到M、N的位置是解决问题的关键,学会利用函数解决点的坐标问题,求最小值时用转化的思想,利用勾股定理去解决,属于中考常考题型.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 在下列坐标系中画出y=x的图象.
在下列坐标系中画出y=x的图象. 如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC,若将纸片沿AE折叠,使点B落在AC上,求AE的长.
如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC,若将纸片沿AE折叠,使点B落在AC上,求AE的长.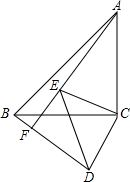 如图,△ABC和△CDE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,AE、BD交于点F,则∠AFB的度数为90°.
如图,△ABC和△CDE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,AE、BD交于点F,则∠AFB的度数为90°.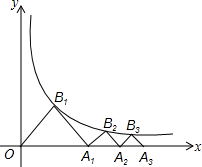 已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.
已知反比例函数$y=\frac{4}{x}$,作等腰Rt△OA1B1,使点B1在反例函数的图象上,点A1在x轴上,再作等腰Rt△A1B2A2,使点B2在反比例函数的图象上,点A2在x轴上;…,再作等腰Rt△A8B9A9,则OA9=12.