题目内容

19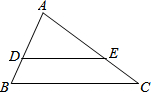．如图，在△ABC中，DE∥BC，AD=3，BD=2，则△ADE与四边形DBCE的面积之比是（　　）
A．3：2B．3：5C．9：16D．9：4

分析 因为DE∥BC，所以可得△ADE∽△ABC，根据相似三角形的面积比等于相似比的平方解答即可．

解答 解：∵AD=3，BD=2，
∴AB=AD+BD=5，
∵D、E分别是△ABC的AB、AC边上的点，DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=（$\frac{3}{5}$）2=$\frac{9}{25}$，
∴△ADE与四边形DBCE的面积之比是：$\frac{9}{16}$，
故选：C．

点评 本题考查了相似三角形的判定与性质，熟知相似三角形面积的比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
9．有18米长的木材，要做成一个如图的窗框．如果假设窗框横档的长度为x米，那么窗框的面积是（　　）
A．x（9-x）米2B．x（18-2x）米2C．x（9-3x）米2D．$x（9-\frac{3}{2}x）$米2
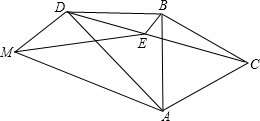10．如图，四边形ABDM中，AB=BD，AB⊥BD，∠AMD=60°，以AB为边作等边△ABC，∠ABD的平分线BE交CD于点E，连接ME．
（1）求∠BEC的度数；
（2）连接EA，求证：EC=ED+EB；
（3）求∠AME的度数．
7．如图，点B（0，b），A（a，0）分别在y轴，x轴正半轴上，满足$\sqrt{a-b}+（ab-16）$2=0．
（1）填空：a=4，b=4，∠OAB的度数是45°；
（2）如图1，已知H（0，1），在第一象限内存在点G，HG交AB于E，使BE为△BHG的中线，且S△BHG=3，求点G的坐标；
（3）如图2，C、D是y轴上两点，且BC=OD，连接AD，过点O作MN⊥AD于点N，交直线AB于点M，连接CM，求∠ADO+∠BCM的值．
14．综合平面直角坐标系，探讨：
（1）点（3，4）和点（4，3）是否关于第一、三象限两坐标轴夹角的平分线对称？
（2）点（3，4）和点（-4，-3）是否关于第二、四象限两坐标轴夹角的平分线对称？
（3）将（1），（2）题的结论推广，点（a，b）关于第一、三象限两坐标轴夹角的平分线的对称点的坐标和关于第二、四象限两坐标轴夹角的平分线的对称点的坐标分别是什么？
4．已知AD为∠BAC的平分线，EF为AD的垂直平分线，求证：FD2=FB•FC．
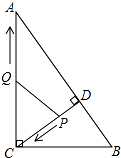11．如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？
8．在同一直角坐标系内画出下列函数的图象：
（1）y=4x-1；
（2）y=4x+1；
（3）y=-4x-1．
9．如图，把圆形纸片沿着一条弦CD翻折，使圆心O在折起的圆弧上，E，O分别是翻折前后的对应点，连接OE．求证：四边形CEDO是菱形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网