题目内容
7.如图,点B(0,b),A(a,0)分别在y轴,x轴正半轴上,满足$\sqrt{a-b}+(ab-16)$2=0.(1)填空:a=4,b=4,∠OAB的度数是45°;
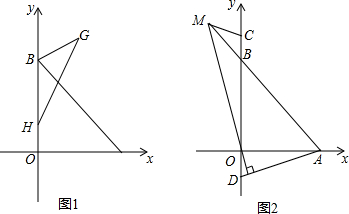
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHG=3,求点G的坐标;
(3)如图2,C、D是y轴上两点,且BC=OD,连接AD,过点O作MN⊥AD于点N,交直线AB于点M,连接CM,求∠ADO+∠BCM的值.
分析 (1)可以非负数的性质得出a、b的方程组,求得a、b即可,进一步得出,∠OAB的度数;
(2)求得直线AB的解析式,表示出E点坐标,利用△BHG的面积得出G点的横坐标,进一步利用中点坐标公式求得点E坐标,得出点G坐标即可;
(3)过点B作BK⊥OC交MN于点K,然后证明△OBK≌△OAD、△MKB≌△MCB,从而可证明∠ADO+∠BCM=180°
解答 解:(1)∵$\sqrt{a-b}+(ab-16)$2=0
∴a-b=0,ab-16=0,
解得:a=4,b=4或a=-4.b=-4,
∵在y轴,x轴正半轴上,
∴a=4,b=4;
∴∠OAB=45°;
(2)如图,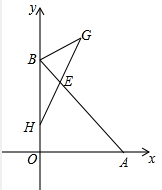
设直线AB解析式为y=kx+b,
代入(0,4),(4,0)解得y=-x+4,
则点E坐标为(x,-x+4),
∵S△BHG=3,BH=3,
∴G点横坐标为2,
∵E为BH的中点,
∴x=$\frac{0+2}{2}$=1,-x+4=3,
∴3=$\frac{1+y}{2}$,解得y=5,
∴点G的坐标为(2,5);
(3)过点B作BK⊥OC交MN于点K.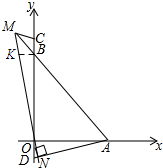
∵MN⊥AD,
∴∠DON+∠NOA=90°.
∴∠KOB+∠NOA=90°.
∵∠NOA+∠NAO=90°,
∴∠KOB=∠DAO.
在△OBK和△OAD中,
$\left\{\begin{array}{l}{∠KBO=∠DOA}\\{OB=OA}\\{∠KOB=∠OAD}\end{array}\right.$,
∴△OBK≌△OAD.
∴KB=OD,∠ODA=∠BKO.
∵BC=OD.
∴KB=BC.
∵∠OB=OA,∠BOA=90°,
∴∠OBA=45°.
∴∠KBM=∠CBM=45°.
在△MKB和△MCB中,
$\left\{\begin{array}{l}{MB=MB}\\{∠KBM=∠DBM}\\{KB=DB}\end{array}\right.$,
∴△MKB≌△MCB.
∴∠MKB=∠MCB.
∵∠OKB+∠MKB=180°,
∴∠ADO+∠BCM=180°.
点评 此题考查坐标与图形的性质,全等三角形的判定及性质的运用,中点坐标公式,三角形的面积,解答时证明三角形全等是关键.

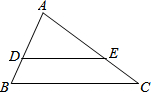 如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )| A. | 3:2 | B. | 3:5 | C. | 9:16 | D. | 9:4 |
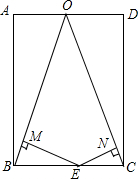 如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.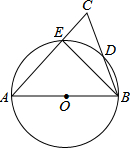 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.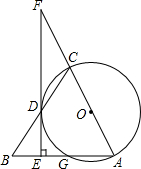 如图,△ABC中,以AC为直径的⊙O与边BC、BA交于点D、G,D是BC的中点,DE⊥AB,垂足为E,ED与AC的延长线交于点F.
如图,△ABC中,以AC为直径的⊙O与边BC、BA交于点D、G,D是BC的中点,DE⊥AB,垂足为E,ED与AC的延长线交于点F.