题目内容
14.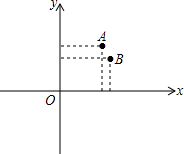 综合平面直角坐标系,探讨:
综合平面直角坐标系,探讨:(1)点(3,4)和点(4,3)是否关于第一、三象限两坐标轴夹角的平分线对称?
(2)点(3,4)和点(-4,-3)是否关于第二、四象限两坐标轴夹角的平分线对称?
(3)将(1),(2)题的结论推广,点(a,b)关于第一、三象限两坐标轴夹角的平分线的对称点的坐标和关于第二、四象限两坐标轴夹角的平分线的对称点的坐标分别是什么?
分析 (1)由图象可知:点(3,4)和点(4,3)关于y=x对称,所以(点(3,4)和点(4,3)关于第一、三象限两坐标轴夹角的平分线对称;
(2)点(3,4)和点(-4,-3)关于y=-x对称,所以点(3,4)和点(-4,-3)关于第二、四象限两坐标轴夹角的平分线对称;
(3)利用(1),(2)得出结论即可.
解答 解:如图,
(1)点(3,4)和点(4,3)关于第一、三象限两坐标轴夹角的平分线对称;
(2)点(3,4)和点(-4,-3)关于第二、四象限两坐标轴夹角的平分线对称;
(3)点(a,b)关于第一、三象限两坐标轴夹角的平分线的对称点的坐标是(b,a);
关于第二、四象限两坐标轴夹角的平分线的对称点的坐标分别是(-b,-a).
点评 此题考查坐标与图形的性质,掌握轴对称图形的特点是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
4.2012年数据统计,成都市常驻人口约为1417万,这个数字用科学记数法表示为( )
| A. | 1.417×103 | B. | 1.417×107 | C. | 1.417×108 | D. | 1417×104 |
19.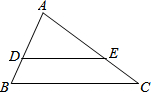 如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
 如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )| A. | 3:2 | B. | 3:5 | C. | 9:16 | D. | 9:4 |
 如图,点P(a,b)是直角坐标系中的一动点,O为坐标原点.
如图,点P(a,b)是直角坐标系中的一动点,O为坐标原点.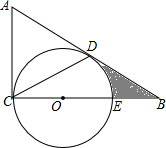 如图,CE是⊙O的直径,AC为⊙0的切线,D为⊙O上的一点,∠A=2∠DCE,延长AD交CE的延长线于点B,连接CD.若BE=OE=2.
如图,CE是⊙O的直径,AC为⊙0的切线,D为⊙O上的一点,∠A=2∠DCE,延长AD交CE的延长线于点B,连接CD.若BE=OE=2.