题目内容
10.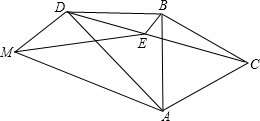 如图,四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.
如图,四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.(1)求∠BEC的度数;
(2)连接EA,求证:EC=ED+EB;
(3)求∠AME的度数.
分析 (1)根据△ABC是等边三角形,得到AB=BC,∠ABC=60°,由AB⊥BD,得到BC=BD,∠DBC=∠ABD+∠ABC=150°,根据等腰三角形的性质得到∠BDC=∠BCD=$\frac{1}{2}$(180°-∠DBC)=15°,又BE平分∠ABD,得到∠DBE=$\frac{1}{2}$∠ABD=45°,利用外角的性质得到∠BEC=∠BDE+∠DBE=15°+45°=60°.
(2)在EC上截取EN=EB,由∠BEC=60°,所以△EBN是等边△,得到BE=BN,证明△BDE≌△BCN,得到DE=CN.所以EC=EN+NC=ED+EB.
(3)连接AE,延长MA至F,使FA=DM,连接EF.先证明△BDE≌△BAE,得到DE=AE,∠BED=∠BEA=180°-∠BEC=120°,再证明△EDM≌△EAF(SAS),得到EM=EF,∠DEM=∠AEF,所以∠DEM+∠AEM=∠AEF+∠AEM,即∠DEA=∠MEF=120°.在△MEF中,∠MEF=120°,EM=EF,所以∠F=∠EMF=30°,即∠AME=30°.
解答 解:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵AB=BD,∠ABD=90°,
∴BC=BD,∠DBC=∠ABD+∠ABC=150°,
∴∠BDC=∠BCD=$\frac{1}{2}$(180°-∠DBC)=15°,
又∵BE平分∠ABD,
∴∠DBE=$\frac{1}{2}$∠ABD=45°,
∴∠BEC=∠BDE+∠DBE=15°+45°=60°.
(2)如图1,在EC上截取EN=EB,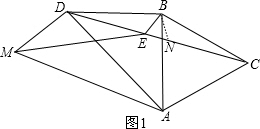
∵∠BEC=60°,
∴△EBN是等边△,
∴BE=BN,
∠CBN=∠DBC-∠DBE-∠EBN=150°-45°-60°=45°=∠DBE,
在△BDE和△BCN中,
$\left\{\begin{array}{l}{DB=CB}\\{∠DBE=∠CBN}\\{BE=BN}\end{array}\right.$,
∴△BDE≌△BCN,
∴DE=CN.
∴EC=EN+NC=ED+EB.
(3)如图2,连接AE,延长MA至F,使FA=DM,连接EF.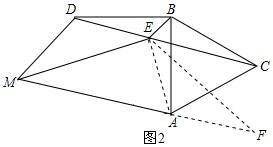
在△BDE与△BAE中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABE}\\{BE=BE}\end{array}\right.$,
∴△BDE≌△BAE,
∴DE=AE,∠BED=∠BEA=180°-∠BEC=120°,
∴∠AED=360°-∠BED-∠BEA=120°.
∴∠AED+∠AMD=120°+60°=180°,
∴∠EAM+∠EDM=180°,
又∠EAM+∠EAF=180°,
∴∠EDM=∠EAF.
在△EDM与△EAF中,
$\left\{\begin{array}{l}{DM=AF}\\{∠EDM=∠EAF}\\{DE=AE}\end{array}\right.$,
∴△EDM≌△EAF(SAS),
∴EM=EF,∠DEM=∠AEF,
∴∠DEM+∠AEM=∠AEF+∠AEM,即∠DEA=∠MEF=120°.
在△MEF中,
∵∠MEF=120°,EM=EF,
∴∠F=∠EMF=30°.
即∠AME=30°.
点评 本题考查了全等三角形的性质和判定、等腰三角形的性质,解决本题的关键是作出辅助线,构建三角形全等.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | x2•x3=x6 | B. | (xn+1)2=x2n+1 | C. | (-2xy2)2=4x2y4 | D. | 2x+x=2x2 |
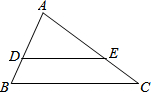 如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )| A. | 3:2 | B. | 3:5 | C. | 9:16 | D. | 9:4 |
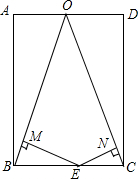 如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.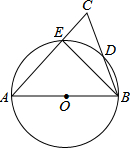 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.