题目内容
18.计算(1)($\sqrt{6}-2\sqrt{15}$)×$\sqrt{3}-6\sqrt{\frac{1}{2}}$
(2)(3$\sqrt{2}-1$)2-$\root{3}{8}$(4-$\sqrt{72}$)
分析 (1)先算乘法,再算加减即可;
(2)先算乘方,开方,再乘法,最后算加减即可.
解答 解:(1)原式=3$\sqrt{2}$-6$\sqrt{5}$-3$\sqrt{2}$
=-6$\sqrt{5}$;
(2)原式=19-6$\sqrt{2}$-2(4-6$\sqrt{2}$)
=19-6$\sqrt{2}$-8+12$\sqrt{2}$
=11+6$\sqrt{2}$.
点评 本题考查的是实数的运算,熟知二次根式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.6把钥匙有2把是开大门和房门的(钥匙大小都相同),某人在黑夜摸出钥匙开门,则他一次成功地打开两道门的概率是(打开大门后钥匙不放回)( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
6.$\sqrt{(-4)^{2}}$的平方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
3.在四个数$\sqrt{3}$,$\sqrt{2}$,1.7,2中,最大的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1.7 | D. | 2 |
10.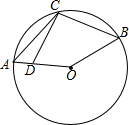 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )| A. | ∠DCB+$\frac{1}{2}$∠O=180° | B. | ∠ACB+$\frac{1}{2}$∠O=180° | C. | ∠ACB+∠O=180° | D. | ∠CAO+∠CBO=180° |
8.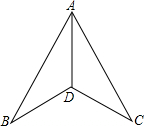 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=CD |