题目内容
5.关于x的一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的根是( )| A. | $\frac{b±\sqrt{b^2-4ac}}{2a}$ | B. | $\frac{-b+\sqrt{b^2-4ac}}{2a}$ | C. | $\frac{-b±\sqrt{b^2-4ac}}{2}$ | D. | $\frac{-b±\sqrt{b^2-4ac}}{2a}$ |
分析 熟记求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,进行选择即可.
解答 解:当a≠0,b2-4ac>0时,
一元二次方程的求根公式为x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,
故选D.
点评 本题考查了用公式法解一元二次方程,解一元二次方程的方法还有,配方法、因式分解法,要熟练掌握.

练习册系列答案
相关题目
16.在Rt△ABC中,若∠C=90°,cosA=$\frac{3}{5}$,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
10.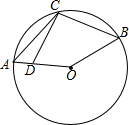 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )| A. | ∠DCB+$\frac{1}{2}$∠O=180° | B. | ∠ACB+$\frac{1}{2}$∠O=180° | C. | ∠ACB+∠O=180° | D. | ∠CAO+∠CBO=180° |
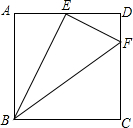 如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.
如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.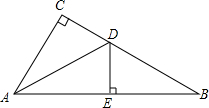 如图,在Rt△ABC中,∠C=90°,DE垂直平分AB分别交BC、AB于点D、E,且CD=DE,求∠B的度数.
如图,在Rt△ABC中,∠C=90°,DE垂直平分AB分别交BC、AB于点D、E,且CD=DE,求∠B的度数.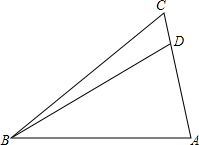 如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.