题目内容
解方程：
（1）x（x+4）=-5（x+4）
（2）（x+2）2=（2x-1）2．
（1）x（x+4）=-5（x+4）
（2）（x+2）2=（2x-1）2．
考点：解一元二次方程-因式分解法
专题：计算题
分析：（1）方程移项后，提取公因式化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解；
（2）利用平方根定义开方转化为两个一元一次方程来求解．
（2）利用平方根定义开方转化为两个一元一次方程来求解．
解答：解：（1）方程移项得：x（x+4）+5（x+4）=0，
分解因式得：（x+5）（x+4）=0，
可得x+4=0或x+5=0，
解得：x1=-4，x2=-5；
（2）开方得：x+2=2x-1或x+2=-2x+1，
解得：x1=3，x2=-
．
分解因式得：（x+5）（x+4）=0，
可得x+4=0或x+5=0，
解得：x1=-4，x2=-5；
（2）开方得：x+2=2x-1或x+2=-2x+1，
解得：x1=3，x2=-
| 1 |
| 3 |
点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=5，则点P到AB的距离是（ ）| A、3 | B、4 | C、5 | D、6 |
如图，已知反比例函数y1=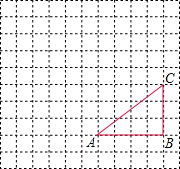
如图，正方形网格中，△ABC为格点三角形（顶点都在格点上），将△ABC绕点A按逆时针方向旋转90°得到△AB1C1．