题目内容
6.操作:将一个边长为1的等边三角形(如图1)的每一边三等分,以居中那条线段为底边向外作等边三角形,并去掉所作的等边三角形的一条边,得到一个六角星(如图2),称为第一次分形.接着对每个等边三角形凸出的部分继续上述过程,即在每条边三等分后的中段向外画等边三角形,得到一个新的图形(如图3),称为第二次分形.不断重复这样的过程,就能得到雪花曲线.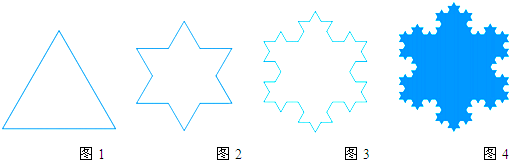
问题:
(1)从图形的对称性观察,图4是中心对称图形又是轴对称图形(轴对称或中心对称图形)
(2)图2的周长为4;
(3)试猜想第n次分形后所得图形的周长为3×($\frac{4}{3}$)n.
分析 (1)根据图形变化规律,图4仍然关于原三角形的对称轴成轴对称,关于对称中心成中心对称;
(2)分形后,三角形的边长增加$\frac{1}{3}$,变为原来的$\frac{4}{3}$,再乘以3就是周长;
(3)每一次分形后,边长都变为原来的$\frac{4}{3}$,第n次分形后边长就变为原来的($\frac{4}{3}$)n倍,再乘以3就是周长.
解答 解:(1)图4是中心对称图形又是轴对称图形.
(2)根据题意,边长为$\frac{1}{3}$×4=$\frac{4}{3}$,
周长为$\frac{4}{3}$×3=4;
(3)n次分形,边长变为原来的($\frac{4}{3}$)n倍,
周长为3×($\frac{4}{3}$)n×1=3×($\frac{4}{3}$)n.
故答案为:中心对称图形又是轴对称图形,4,3×($\frac{4}{3}$)n.
点评 此题考查图形的变化规律,找出图形之间的联系,得出运算规律解决问题.

练习册系列答案
相关题目
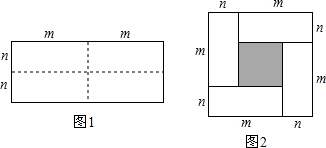
1.某商场计划购进两种服装共100件,这两种服装的进价、售价如表所示:
(1)若商场预计进货用3500元,则这两种服装个购进多少件?
(2)若商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍,求商场有几种进货方案;
(3)在(2)条件下应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?
| 价格 类型 | 进价(元/件) | 售价(元/件) |
| A | 30 | 45 |
| 售价(元/部) | 50 | 70 |
(2)若商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍,求商场有几种进货方案;
(3)在(2)条件下应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?
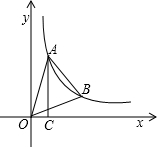 如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.
如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.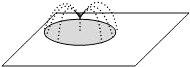 要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面.则需安装这种喷水龙头的个数最少是4个.
要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面.则需安装这种喷水龙头的个数最少是4个.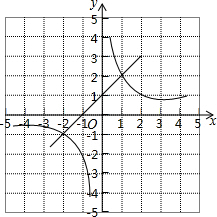 一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1.
一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1.