题目内容
11．
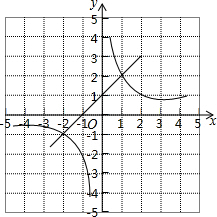一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示，则使kx+b$＞\frac{2}{x}$的x的取值范围是-2＜x＜0或x＞1．
分析 观察函数图象，先写出两函数的交点坐标，由于当-2＜x＜0或x＞1时，直线y=kx+b都在y=$\frac{2}{x}$的图象上方，于是可得kx+b$＞\frac{2}{x}$的x的取值范围．
解答 解：一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象的交点坐标为（-2，-1）、（1，2），
所以当-2＜x＜0或x＞1时，kx+b$＞\frac{2}{x}$．
故答案为-2＜x＜0或x＞1．
点评 本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AB是⊙O的直径，PB是⊙O的切线，PA交⊙O于C，AB=6cm，PB=8cm，则BC=4.8cm．
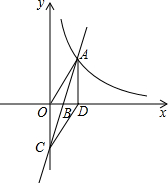如图，直线y=kx-3（k＞0）与x轴交于点B，与y轴的交于点C，与双曲线y=$\frac{k}{x}$在第一象限内的交点为点A，过点A作AD⊥x轴于点D，若四边形OADC是平行四边形，则k=3$\sqrt{2}$．
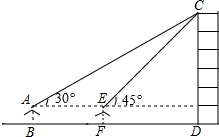小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414．结果保留整数）