题目内容
在函数y=
的图象上有A(-2,y1)、B(-1,y2)、C(3,y3)三点,则函数值y1、y2、y3的大小关系是( )
| -k2 |
| x |
| A、y3<y2<y1 |
| B、y2<y3<y1 |
| C、y1<y2<y3 |
| D、y3<y1<y2 |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:分别计算出自变量为-2、-1和3的函数值,然后比较函数值的大小即可.
解答:解:当x=-2时,y1=
=
;当x=-1时,y2=
=k2;当x=3时,y3=
=-
,
所以y3<y2<y1.
故选A.
| -k2 |
| x |
| k2 |
| 2 |
| -k2 |
| x |
| -k2 |
| x |
| k2 |
| 9 |
所以y3<y2<y1.
故选A.
点评:本题考查了反比例函数图象点的坐标特征:反比例函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )
| A、120°,60° |
| B、95°,105° |
| C、30°,60° |
| D、90°,90° |
下列函数关系式中,y是x的二次函数是( )
| A、y=ax2+bx+c | ||
B、y=x2-
| ||
C、y=
| ||
| D、y=(3x+2)(4x-3)-12x2 |
已知A(
,y1),B(2,y2),C(-
,y3)是二次函数y=3(x-1)2+k图象上三点,则y1、y2、y3的大小关系为( )
| 2 |
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y2>y1 |
| D、y2>y3>y1 |
已知反比例函数y=
的图象在一、三象限,那么直线y=kx-k不经过第( )象限.
| k |
| x |
| A、一 | B、二 | C、三 | D、四 |
 一住宅楼发生火灾,消防车立即赶到,准备在距大厦6米处升起云梯到火灾窗口展开营救,已知云梯AB伸长后的最大长度为12米,云梯底部B距地面2米,此时消防队员能否成功救下等候在距离地面约10米窗口的受困人群?说说你的理由.
一住宅楼发生火灾,消防车立即赶到,准备在距大厦6米处升起云梯到火灾窗口展开营救,已知云梯AB伸长后的最大长度为12米,云梯底部B距地面2米,此时消防队员能否成功救下等候在距离地面约10米窗口的受困人群?说说你的理由.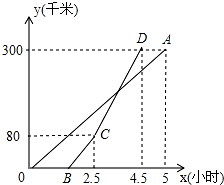 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题: 两个同样大小的正方体积木,每个正方体相对两个面上写的数字之和都等于0.现将两个正方体并排放置,看得见的5个面上的数如图所示,则看不见的7个面上所写的数字之和等于
两个同样大小的正方体积木,每个正方体相对两个面上写的数字之和都等于0.现将两个正方体并排放置,看得见的5个面上的数如图所示,则看不见的7个面上所写的数字之和等于