题目内容
 一住宅楼发生火灾,消防车立即赶到,准备在距大厦6米处升起云梯到火灾窗口展开营救,已知云梯AB伸长后的最大长度为12米,云梯底部B距地面2米,此时消防队员能否成功救下等候在距离地面约10米窗口的受困人群?说说你的理由.
一住宅楼发生火灾,消防车立即赶到,准备在距大厦6米处升起云梯到火灾窗口展开营救,已知云梯AB伸长后的最大长度为12米,云梯底部B距地面2米,此时消防队员能否成功救下等候在距离地面约10米窗口的受困人群?说说你的理由.考点:勾股定理的应用
专题:
分析:先根据题意建立直角三角形,然后利用勾股定理求出AB的长度,最后求出云梯的长度比较即可得出答案.
解答: 解:能.
解:能.
理由:由题意得,BC=6米,AC=10-2=8(米),
在RT△ABC中,AB2=AC2+BC2,即可得AB2=82+62=64+36=100,
而122=144>100,
故能救下.
 解:能.
解:能.理由:由题意得,BC=6米,AC=10-2=8(米),
在RT△ABC中,AB2=AC2+BC2,即可得AB2=82+62=64+36=100,
而122=144>100,
故能救下.
点评:此题主要考查了勾股定理的应用,根据题意正确得出各部分的长是解题关键.

练习册系列答案
相关题目
根据图中数字的规律,最后一个空格应填的数是( )

| A、738 | B、720 |
| C、550 | D、500 |
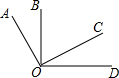 如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,如果各边的长度都缩小至原来的
,那么锐角A的各个三角函数值( )
| 1 |
| 4 |
A、都缩小
| ||
| B、都扩大4倍 | ||
| C、都不变 | ||
| D、无法确定 |
在函数y=
的图象上有A(-2,y1)、B(-1,y2)、C(3,y3)三点,则函数值y1、y2、y3的大小关系是( )
| -k2 |
| x |
| A、y3<y2<y1 |
| B、y2<y3<y1 |
| C、y1<y2<y3 |
| D、y3<y1<y2 |
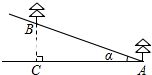 如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.5米范围内,问小明种植的这两棵树是否符合这个要求?