题目内容
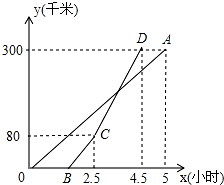 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:(1)求线段CD对应的函数解析式.
(2)货车从甲地出发后多长时间被轿车追上?此时离甲地的距离是多少千米?
(3)轿车到达乙地后,货车距乙地多少千米.
考点:一次函数的应用
专题:
分析:(1)设线段CD对应的函数解析式为y=kx+b,由待定系数法求出其解即可;
(2)设OA的解析式为y货=k1x,由待定系数法求出解析式,由一次函数与一元一次方程的关系建立方程求出其解即可.
(3)先由函数图象求出货车在轿车到达乙地是时需要的时间,由路程=速度×时间就可以求出结论.
(2)设OA的解析式为y货=k1x,由待定系数法求出解析式,由一次函数与一元一次方程的关系建立方程求出其解即可.
(3)先由函数图象求出货车在轿车到达乙地是时需要的时间,由路程=速度×时间就可以求出结论.
解答:解:(1)设线段CD对应的函数解析式为y=kx+b,由题意,得
,
解得:
.
则y=110x-195.
答:线段CD对应的函数解析式为y=110x-195;
(2)设OA的解析式为y货=k1x,由题意,得
300=5k1,
解得:k1=60,
∴y货=60x.
∴当y=y货时,
110x-195=60x,
解得:x=3.9.
离甲地的距离是:3.9×60=234千米.
答:货车从甲地出发后3.9小时被轿车追上,此时离甲地的距离是234千米;
(3)由题意,得
60×(5-4.5)=30千米.
答:轿车到达乙地后,货车距乙地30千米.
|
解得:
|
则y=110x-195.
答:线段CD对应的函数解析式为y=110x-195;
(2)设OA的解析式为y货=k1x,由题意,得
300=5k1,
解得:k1=60,
∴y货=60x.
∴当y=y货时,
110x-195=60x,
解得:x=3.9.
离甲地的距离是:3.9×60=234千米.
答:货车从甲地出发后3.9小时被轿车追上,此时离甲地的距离是234千米;
(3)由题意,得
60×(5-4.5)=30千米.
答:轿车到达乙地后,货车距乙地30千米.
点评:本题考查了一次函数的图象的性质的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
根据图中数字的规律,最后一个空格应填的数是( )

| A、738 | B、720 |
| C、550 | D、500 |
在Rt△ABC中,如果各边的长度都缩小至原来的
,那么锐角A的各个三角函数值( )
| 1 |
| 4 |
A、都缩小
| ||
| B、都扩大4倍 | ||
| C、都不变 | ||
| D、无法确定 |
已知二次函数y=2x2+1.下列说法:
①其图象的开口向下;
②其图象的对称轴为y轴;
③其图象顶点坐标为(2,1);
④当x<0时,y随x的增大而减小.
则其中说法正确的有( )
①其图象的开口向下;
②其图象的对称轴为y轴;
③其图象顶点坐标为(2,1);
④当x<0时,y随x的增大而减小.
则其中说法正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
多项式x2-3x+a可分解为(x-5)(x-b),则a、b的值分别是( )
| A、10和-2 |
| B、-10和2 |
| C、10和2 |
| D、-10和-2 |
在函数y=
的图象上有A(-2,y1)、B(-1,y2)、C(3,y3)三点,则函数值y1、y2、y3的大小关系是( )
| -k2 |
| x |
| A、y3<y2<y1 |
| B、y2<y3<y1 |
| C、y1<y2<y3 |
| D、y3<y1<y2 |
下列函数中,图象经过原点的有( )
①y=2x-2;②y=5x2-4x;③y=-x2;④y=
.
①y=2x-2;②y=5x2-4x;③y=-x2;④y=
| 6 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
 小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料,小聪骑电动车,小明骑自行车,当小聪从原路回到学校时,小明刚好到市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(小时)之间的函数关系,请根据图象回答下列问题:
小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料,小聪骑电动车,小明骑自行车,当小聪从原路回到学校时,小明刚好到市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(小时)之间的函数关系,请根据图象回答下列问题: