题目内容
2. 如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.
如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据:$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{6}$=2.4).
分析 (1)延长BA交EF于点G.根据三角形内角和定理求出∠CAE的度数;
(2)过点A作AE⊥CD,根据余弦和正弦的概念分别求出DH和AH的长,根据等腰直角三角形的性质计算即可.
解答 解:(1)延长BA交EF于点G.
在Rt△AGE中,∠E=23°,
∴∠GAE=67°,
又∵∠BAC=38°,
∴∠CAE=180°-67°-38°=75°.
(2)过点A作AE⊥CD,垂足为H.
在△ADH中,∠ADC=60°,AD=8,
cos∠ADC=$\frac{DH}{AD}$,
∴DH=4,
sin∠ADC=$\frac{AH}{AD}$,
∴$AH=4\sqrt{3}$.
在Rt△ACH中,∠C=180°-75°-60°=45°,
∴$CH=AH=4\sqrt{3}$,$AC=4\sqrt{6}$.
∴$AB=AC+CD=4\sqrt{6}+4\sqrt{3}+4≈20$(米).
答:这棵大树折断前高约20米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,正确标注坡角、倾斜角、灵活运用锐角三角函数的概念是解题的关键,注意特殊角的三角函数值的应用.

练习册系列答案
相关题目
12.一汽车租赁公司拥有某种型号的汽车50辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数y(辆)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接判断每月租出的车辆数y(辆)与每辆车的月租金x(元)之间满足三类函数关系中的哪类函数关系,并求出y与x之间的关系式(写出自变量x的取值范围).
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
| x | … | 10800 | 11000 | 11200 | 11400 | … |
| y | … | 30 | 25 | 20 | 15 | … |
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
10.小林在某商店购买商品A,B共三次,第一、两次均按标价购物,第三次购物时,商品A,B同时打6折,三次购物商品A,B的数量和费用如下表:
(1)求出商品A,B的标价;
(2)求第三次购物时的总费用是多少?
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 |
(2)求第三次购物时的总费用是多少?
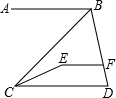 如图,已知AB∥CD,AB∥EF.
如图,已知AB∥CD,AB∥EF. 某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.
某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.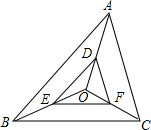 如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.
如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC. 如图,有一块塑料矩形模板ABCD,长为10cm,宽为5cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A,D重合),在AD上适当移动三角板顶点P,能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.
如图,有一块塑料矩形模板ABCD,长为10cm,宽为5cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A,D重合),在AD上适当移动三角板顶点P,能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.