Question

13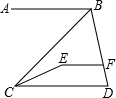．如图，已知AB∥CD，AB∥EF．
（1）判断CD和EF是否平行，若平行，说明平行的依据是平行公理的推论．
（2）∠ABC与哪些角是内错角？∠ABD与哪些角是同旁内角？
（3）若CE平分∠BCD，∠ABC=46°，试求∠CEF的度数．

Answer 1

分析 （1）根据平行公理的推论，直接判断即可；
（2）根据内错角、同旁内角的定义，直接解答即可；
（3）根据平行的性质，求出∠BCD的度数，根据角平分线的定义，求出∠ECD的度数，根据平行线的性质，即可解答．

解答 解：（1）CD平行EF，依据是：平行公理的推论；
（2）∠ABC的内错角有：∠BCD，∠BCE；
∠ABD的同旁内角有：∠BFD，∠BDC；
（3）∵AB∥CD，∠ABC=46°，
∴∠BCD=∠ABC=46°，
∵CE平分∠BCD，
∴∠ECD=$\frac{1}{2}$∠BCD=23°，
由（1）可知，CD∥EF，
∴∠CEF+∠ECD=180°，
∴∠CEF=180°-∠ECD=180°-23°=157°．

点评 本题主要考查平行线的性质和判断及从复杂图形中找到同位角、内错角、同旁内角，解决第（2）小题的关键是能把复杂图形简单化，第（3）小题，需要灵活运用平行线的性质．