题目内容
16.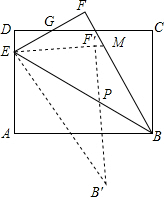 如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
分析 如图先证明DH=EF=AE,设AE=EF=DH=x,在RT△BCH中利用勾股定理求出x,再利用△EAN∽△BAE得$\frac{AE}{AB}$=$\frac{AN}{AE}$即可解决问题.
解答 解:设AE=EF=x,
∵四边形ABCD是矩形,
∴AB=CD=10,AD=BC=7.5,∠A=∠D=∠C=90°,
在△DGE和△FGH中,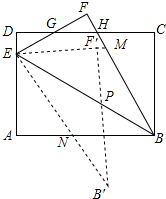
$\left\{\begin{array}{l}{∠D=∠F=90°}\\{∠DGE=∠FGH}\\{DG=GF}\end{array}\right.$,
∴△DGE≌△FGH,
∴EG=GH,DE=FH,
∴DH=EF=x,DE=FH=7.5-x,BH=10-FH=2.5+x,CH=10-x
在RT△BCH中,∵BH2=CH2+BC2,
∴(2.5+x)2=(10-x)2+7.52,
∴x=6,
∴AE=6,
∵EM=MB,
∴∠MEB=∠MBE=∠EBA=∠AEN,∵∠EAN=∠EAB=90°,
∴△EAN∽△BAE,
∴$\frac{AE}{AB}$=$\frac{AN}{AE}$,
∴$\frac{6}{10}$=$\frac{AN}{6}$,
∴AN=$\frac{18}{5}$.
故答案为$\frac{18}{5}$.
点评 本题考查翻折变换、旋转变换、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是设未知数利用方程解决问题,属于中考常考题型.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
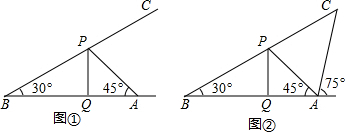
4. 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )
 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )| A. | ∠2+∠3=180° | B. | ∠1=∠4 | C. | ∠2+∠4=180° | D. | ∠2=∠3 |
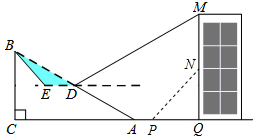 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.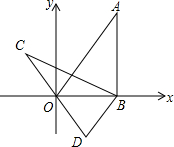 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).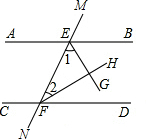 如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?
如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?