题目内容
7.小唐同学在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.(1)如图①,已知旗杆PQ高为10米,若在B处测得旗杆顶点P的仰角为30°,在A处测得点P的仰角为45°,求A,B之间的距离;
(2)如图②,在(1)的条件下,在A处测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC的长.
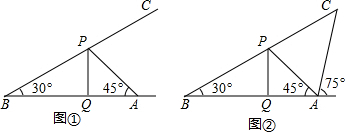
分析 (1)首先分析图形:根据题意构造直角三角形在直角三角形△BPQ中求出AQ的长度,然后求出AB=BQ+AQ;
(2)过A作AE⊥BC于E,在Rt△ABE中,求出AE的长度,然后在△CAE中求出AC的长度;
解答 解:(1)在Rt△BPQ中,PQ=10米,∠B=30°,
∴∠BPQ=90°-30°=60°,
则BQ=tan60°×PQ=10$\sqrt{3}$,
又在Rt△APQ中,∠PAB=∠APQ=45°,
则AQ=tan45°×PQ=10,
即AB=10$\sqrt{3}$+10(米);
(2)过A作AE⊥BC于E,
在Rt△ABE中,∠B=30°,AB=10$\sqrt{3}$+10,
∴AE=sin30°×AB=$\frac{1}{2}$(10$\sqrt{3}$+10)=5$\sqrt{3}$+5(米).
∵∠CAD=75°,∠B=30°,
∴∠C=45°,
在Rt△CAE中,sin45°=$\frac{AE}{AC}$,
∴AC=$\frac{AE}{sin45°}$=$\frac{5\sqrt{3}+5}{\frac{\sqrt{2}}{2}}$=5$\sqrt{6}$+5$\sqrt{2}$(米).
点评 本题考查了解直角三角形的应用,解答本题的关键是结合图形构造直角三角形,利用三角函数解直角三角形.

练习册系列答案
相关题目
20.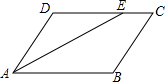 如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )
如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )
 如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )
如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 1.5 |
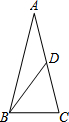 如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.
如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.
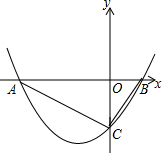 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.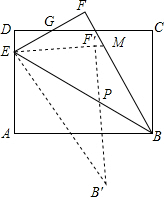 如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.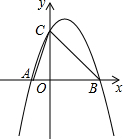 已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:
已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则: