题目内容
13.已知直线y=x+$\frac{3}{2}$与直线y=kx-1相交于点P,若点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集为( )| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
分析 先把y=$\frac{1}{2}$代入y=x+$\frac{3}{2}$,得出x=-1,再观察函数图象得到当x>-1时,直线y=x+$\frac{3}{2}$都在直线y=kx-1的上方,即不等式x+4>kx-1的解集为x>-1,然后用数轴表示解集.
解答 解:把y=$\frac{1}{2}$代入y=x+$\frac{3}{2}$,得
$\frac{1}{2}$=x+$\frac{3}{2}$,解得x=-1.
当x>-1时,x+$\frac{3}{2}$>kx-1,
所以关于x的不等式x+$\frac{3}{2}$>kx-1的解集为x>-1,
故选A
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.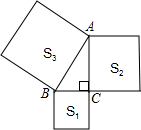 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )| A. | 15 | B. | 225 | C. | 81 | D. | 25 |
4.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |
1.点(-1,a2+1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8. 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )| A. | $\frac{8π}{3}-2\sqrt{3}$ | B. | $\frac{4π}{3}-\sqrt{3}$ | C. | $\frac{8π}{3}-3\sqrt{3}$ | D. | 4$π-\frac{9\sqrt{3}}{4}$ |
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )
| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
2.点A(2,y1)、B(3,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
 如图,在△ABC中,过点B作EB⊥AB,交AC于点E,BE平分∠CBD,90°+∠C=∠BDC,则∠A的度数为45°.
如图,在△ABC中,过点B作EB⊥AB,交AC于点E,BE平分∠CBD,90°+∠C=∠BDC,则∠A的度数为45°.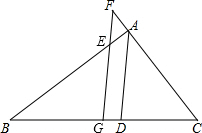 如图,AD是△ABC的角平分线,G是BC中点,FG∥AD,交AB于E,交CA的延长线于F,AC=3.8,AB=7.4,则AF=1.8.
如图,AD是△ABC的角平分线,G是BC中点,FG∥AD,交AB于E,交CA的延长线于F,AC=3.8,AB=7.4,则AF=1.8.