题目内容
16.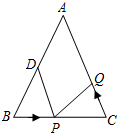 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,D为AB的中点,点P在线段BC上以3厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,D为AB的中点,点P在线段BC上以3厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.(1)若点Q的运动速度与点P的运动速度相等,则1秒后,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
分析 (1)求出BP、CQ、CP,根据全等三角形的判定推出即可;
(2)设当点Q的运动速度为x厘米/时,时间是t小时,能够使△BPD与△CQP全等,求出BD=5厘米,BP=3t厘米,CP=(8-3t)厘米,CQ=xt厘米,∠B=∠C,根据全等三角形的性质得出方程,求出方程的解即可.
解答 解:(1)点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP全等,
理由是:∵AB=AC=10厘米,点D为AB的中点,
∴∠B=∠C,BD=5厘米,
∵BP=CQ=3t厘米=3厘米,
∴CP=8厘米-3厘米=5厘米=BD,
在△DBP和△PCQ中,
$\left\{\begin{array}{l}{BD=CP}\\{∠B=∠C}\\{PB=CQ}\end{array}\right.$,
∴△DBP≌△PCQ(SAS);
(2)设当点Q的运动速度为x厘米/时,时间是t小时,能够使△BPD与△CQP全等,
∵BD=5厘米,BP=3t厘米,CP=(8-3t)厘米,CQ=xt厘米,∠B=∠C,
∴当BP=CQ,BD=CP或BP=CP,BD=CQ时,△BPD与△CQP全等,
即①3t=xt,5=8-3t,
解得:x=3(不合题意,舍去),
②3t=8-3t,5=xt,
解得:x=$\frac{15}{4}$,
即当点Q的运动速度为$\frac{15}{4}$厘米/时时,能够使△BPD与△CQP全等.
点评 本题考查了全等三角形的判定和性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,用了分类讨论思想.

练习册系列答案
相关题目
4.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |
1.点(-1,a2+1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8. 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )| A. | $\frac{8π}{3}-2\sqrt{3}$ | B. | $\frac{4π}{3}-\sqrt{3}$ | C. | $\frac{8π}{3}-3\sqrt{3}$ | D. | 4$π-\frac{9\sqrt{3}}{4}$ |
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )
| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
6.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
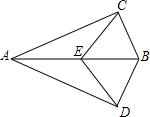 如图,已知:∠ACB和∠ADB都是直角,BC=BD,E是AB上任一点,求证:CE=DE.
如图,已知:∠ACB和∠ADB都是直角,BC=BD,E是AB上任一点,求证:CE=DE.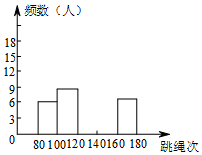 体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示: