题目内容
1.某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示.| 甲种客车 | 乙种客车 | |
| 载客量/(人/辆) | 45 | 30 |
| 租金/(元/辆) | 400 | 280 |
(2)请给出最节省费用的租车方案.
分析 (1)由师生总数为240人,根据“所需租车数=人数÷载客量”算出租载客量最大的客车所需辆数,再结合每辆车上至少要有1名教师,即可得出结论;
(2)设租乙种客车x辆,则甲种客车(6-x)辆,根据师生总数为240人以及租车总费用不超过2300元,即可得出关于x的一元一次不等式,解不等式即可得出x的值,再设租车的总费用为y元,根据“总费用=租A种客车所需费用+租B种客车所需费用”即可得出y关于x的函数关系式,根据一次函数的性质结合x的值即可解决最值问题.
解答 解:(1)∵(234+6)÷45=5(辆)…15(人),
∴保证240名师生都有车坐,汽车总数不能小于6;
∵只有6名教师,
∴要使每辆汽车上至少要有1名教师,汽车总数不能大于6;
综上可知:共需租6辆汽车.
(2)设租乙种客车x辆,则甲种客车(6-x)辆,
由已知得:$\left\{\begin{array}{l}{30x+45×(6-x)≥240}\\{280x+400×(6-x)≤2300}\end{array}\right.$,
解得:$\frac{5}{6}$≤x≤2,
∵x为整数,
∴x=1,或x=2.
设租车的总费用为y元,
则y=280x+400×(6-x)=-120x+2400,
∵-120<0,
∴当x=2时,y取最小值,最小值为2160元.
故租甲种客车4辆、乙种客车2辆时,所需费用最低,最低费用为2160元.
点评 本题考查了一次函数的应用、解一元一次不等式组已经一次函数的性质,解题的关键是:(1)根据数量关系确定租车数;(2)找出y关于x的函数关系式.本题属于中档题,难度不大,解决该题型题目时,根据数量关系找出函数关系式(不等式或不等式组)是关键.

练习册系列答案
相关题目
12. 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转到角度为( )
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转到角度为( )
 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转到角度为( )
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转到角度为( )| A. | 30° | B. | 45° | C. | 90° | D. | 135° |
9.若a,b是方程x2-2x-5=0的两个根,则$\frac{1}{a}$+$\frac{1}{b}$的值为( )
| A. | -$\frac{2}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{5}{2}$ | D. | $\frac{5}{2}$ |
10.下列正多边形的组合中,能够铺满地面的是( )
| A. | 正三角形和正五边形 | B. | 正方形和正六边形 | ||
| C. | 正三角形和正六边形 | D. | 正五边形和正八边形 |
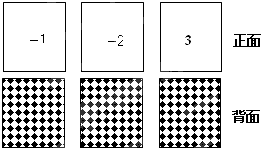 有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.