题目内容
13.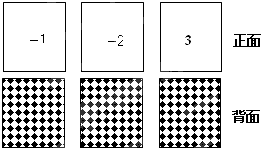 有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.
有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.(1)求出k为负数的概率;
(2)求一次函数y=kx+b的图象经过二、三、四象限的概率.(用树状图或列表法求解)
分析 (1)利用概率的计算方法解答;
(2)画出树状图,共有6种情况,其中满足一次函数y=kx+b经过第二、三、四象限的结果有2个,求出概率即可.
解答 解:(1)∵共有3张牌,两张为负数,
∴k为负数的概率是$\frac{2}{3}$;
(2)画树状图: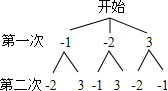 共有6种情况,其中满足一次函数y=kx+b经过第二、三、四象限,
共有6种情况,其中满足一次函数y=kx+b经过第二、三、四象限,
即k<0,b<0的情况有2种,
所以一次函数y=kx+b经过第二、三、四象限的概率为$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了用树状图或列表法、概率公式、一次函数的图象;一次函数y=kx+b的图象与系数的关系;熟练掌握树状图法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列各式中,计算正确的是( )
| A. | 3$\sqrt{3}$+3=6$\sqrt{3}$ | B. | $\frac{1}{7}$$\sqrt{7}$=1 | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | $\sqrt{2}$×2$\sqrt{2}$=4 |
4.如图图形中哪个是正方体的表面展开图?( )
| A. |  | B. |  | C. |  | D. |  |
1.某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
(1)共需租多少辆汽车?
(2)请给出最节省费用的租车方案.
| 甲种客车 | 乙种客车 | |
| 载客量/(人/辆) | 45 | 30 |
| 租金/(元/辆) | 400 | 280 |
(2)请给出最节省费用的租车方案.
8.将函数y=-3x+1沿y轴向上平移4个单位长度后,所得图象对应的函数关系式为( )
| A. | y=-3(x+4)+1 | B. | y=-(x-4)+1 | C. | y=-3x+5 | D. | y=-3x-3 |
18.下列命题是假命题的是( )
| A. | 同位角相等,两直线平行 | B. | 两直线平行,同旁内角相等 | ||
| C. | 若a=b,则|a|=|b| | D. | 若ab=0,则a=0或b=0 |
5.为庆祝“六一”儿童节,某班学生准备分组外出活动,若每组8人,则余下2人;若每组9人,则少5人,求该班人数x和应分成的组数y,依题意得方程组为( )
| A. | $\left\{\begin{array}{l}{8y=x+2}\\{9y+5=x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{8y+2=x}\\{9y=x-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{8y=x-2}\\{9y=x+5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{8y=x+2}\\{9y=x+5}\end{array}\right.$ |
2.方程3x=-6的解是( )
| A. | x=-2 | B. | x=-3 | C. | x=-6 | D. | x=3. |
3. 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )| A. | $\frac{25}{3}$ | B. | 4 | C. | $\frac{25}{6}$ | D. | 5 |