题目内容
11．写出一个以0，1为根的一元二次方程x2-x=0．分析 先根据1+0=1，1×0=0，然后根据根与系数的关系写出满足条件的一个一元二次方程．
解答 解：∵1+0=1，1×0=0，
∴以1和0的一元二次方程可为x2-x=0．
故答案为x2-x=0．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
练习册系列答案
期末集结号系列答案
相关题目
1．某学校计划在总费用2300元的限额内，租用汽车送234名学生和6名教师集体外出活动，每辆汽车上至少要有1名教师．现有甲、乙两种大客车，它们的载客量和租金如表所示．
（1）共需租多少辆汽车？
（2）请给出最节省费用的租车方案．
| 甲种客车 | 乙种客车 | |
| 载客量/（人/辆） | 45 | 30 |
| 租金/（元/辆） | 400 | 280 |
（2）请给出最节省费用的租车方案．
2．方程3x=-6的解是（ ）
| A． | x=-2 | B． | x=-3 | C． | x=-6 | D． | x=3． |
19．下列运算正确的是（ ）
| A． | a3•a2=a6 | B． | （a2）3=a6 | C． | （-2a）3=-2a3 | D． | a3+a3=2a6 |
6．一个寻宝游戏的寻宝通道由正方形ABCD的边组成，如图1所示．为记录寻宝者的行进路线，在AB的中点M处放置了一台定位仪器，设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为（ ）
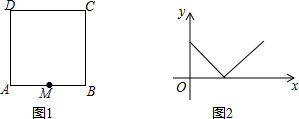
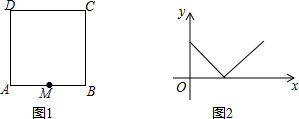
| A． | A→B | B． | B→C | C． | C→D | D． | D→A |
3．
如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F．若AB=6，BC=10，则FD的长为（ ）
如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F．若AB=6，BC=10，则FD的长为（ ）| A． | $\frac{25}{3}$ | B． | 4 | C． | $\frac{25}{6}$ | D． | 5 |
20．某种计算机完成一次基本运算的时间约为0.000000003秒，把数据0.000000003用科学记数法表示为（ ）
| A． | 0.3×10-8 | B． | 0.3×10-9 | C． | 3×10-8 | D． | 3×10-9 |
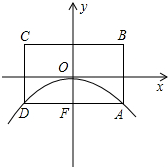如图所示，矩形ABCD的对称中心和抛物线的顶点均为坐标原点O，点A，D在抛物线上．且AD平行x轴，交y轴于点F，点B的坐标为（2，1）．