题目内容
7.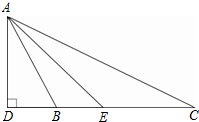 如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.
如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.求证:∠DAE=$\frac{1}{2}$(∠ABC-∠C).
分析 先根据外角性质得:∠ABC=∠D+∠DAB,则∠DAB=∠ABC-∠D=∠ABC-90°,再表示出∠BAE=$\frac{1}{2}$∠BAC,由三角形的内角和定理可得:∠BAE=90°-$\frac{1}{2}$∠ABC-$\frac{1}{2}$∠C,最后利用角的和:∠DAE=∠DAB+∠BAE,代入可得结论.
解答 证明:∵AD⊥BC,
∴∠D=90°,
∵∠ABC是△ABD的外角,
∴∠DAB=∠ABC-∠D=∠ABC-90°,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC,
在△ABC中,∠BAC=180°-∠ABC-∠C,
∴∠BAE=90°-$\frac{1}{2}$∠ABC-$\frac{1}{2}$∠C,
∵∠DAE=∠DAB+∠BAE,
∴∠DAE=∠ABC-90°+90°-$\frac{1}{2}$∠ABC-$\frac{1}{2}$∠C=$\frac{1}{2}$∠ABC-$\frac{1}{2}$∠C,
即:∠DAE=$\frac{1}{2}$(∠ABC-∠C).
点评 本题考查了三角形的内角和、外角性质和角平分线的性质,本题有难度,运用几个角和等式的互换,这就需要熟练掌握内角和定理及三角形的外角性质.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
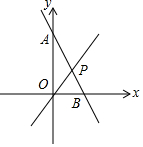 如图,已知一条直线经过点A(0,4)、点B(2,0).
如图,已知一条直线经过点A(0,4)、点B(2,0).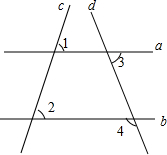 直线a,b,c,d的位置如图所示,已知∠1=58°,∠2=58°,∠3=70°,求∠4的度数.
直线a,b,c,d的位置如图所示,已知∠1=58°,∠2=58°,∠3=70°,求∠4的度数.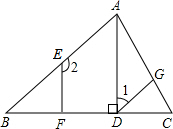 如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数.
如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数. 如图,已知∠1=∠2,∠3=50°,求∠4的大小.
如图,已知∠1=∠2,∠3=50°,求∠4的大小.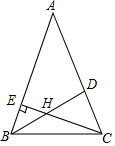 在△ABC中,∠ABC=∠ACB=2∠A,BD是∠ABC的平分线,交AB边上的高CE于点H,求∠BHC的度数.
在△ABC中,∠ABC=∠ACB=2∠A,BD是∠ABC的平分线,交AB边上的高CE于点H,求∠BHC的度数.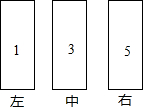 如图所示,三根音管被敲击时能依次发出“1”“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击这三根音管,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…).第2012拍时,听到相同的音,这个相同的音是3.
如图所示,三根音管被敲击时能依次发出“1”“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击这三根音管,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…).第2012拍时,听到相同的音,这个相同的音是3.