题目内容
13.已知正方形ABCD的面积为2,建立直角坐标系,使顶点A、B、C、D的坐标都是有理数,画出示意图并作简要说明.分析 因为正方形ABCD的面积为2,可以得边长为$\sqrt{2}$,则对角线为2,根据正方形的对角线平分得:OA=OB=OC=OD=1,由此得出各顶点的坐标.
解答 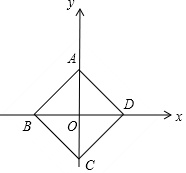 解:如图,以对角线AC、BD所在的直线分别为y轴、x轴,对角线的交点O为坐标原点,建立平面直角坐标系,
解:如图,以对角线AC、BD所在的直线分别为y轴、x轴,对角线的交点O为坐标原点,建立平面直角坐标系,
∵正方形ABCD的面积为2,
∴AB=AD=$\sqrt{2}$,∠BAD=90°
由勾股定理得:BD=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2
∴OA=OB=OC=OD=1
∴A(0,1),B(-1,0),C(0,-1),D(1,0).
点评 本题主要考查了正方形的性质和坐标与图形特点,正方形的各边相等,且四个角都是直角,可以利用勾股定理计算其它线段的长,也可以利用正方形面积=对角线乘积的一半,直接利用面积求对角线的长.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
5.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息:
(说明:①每户产生的污水量等于该户的自来水用水量,②水费=自来水费用+污水处理费;
已知小王家2015年5月份用水20吨,交水费66元;6月份用水25吨,交水费91元.
(1)求a、b的值.
(2)随着夏天的到来,用水量将增加,为了节省开支,小王计划把7月份水费控制在不超过家庭月收入的2%,若小王家的月收入为9600元,则小王家7月份最多能用水多少吨?(结果精确到1吨)
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨但不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
已知小王家2015年5月份用水20吨,交水费66元;6月份用水25吨,交水费91元.
(1)求a、b的值.
(2)随着夏天的到来,用水量将增加,为了节省开支,小王计划把7月份水费控制在不超过家庭月收入的2%,若小王家的月收入为9600元,则小王家7月份最多能用水多少吨?(结果精确到1吨)
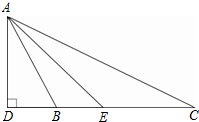 如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.
如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.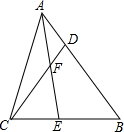 已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.
已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.