题目内容
15.已知:x=$\sqrt{2}$+1,y=$\sqrt{2}$-1,求下列各式的值:(1)x2-y2
(2)x2+2xy+y2.
分析 (1)根据题目中x、y的值代入所求式子,即可解答本题;
(2)根据题目中x、y的值代入所求式子,即可解答本题.
解答 解:(1)∵x=$\sqrt{2}$+1,y=$\sqrt{2}$-1,
∴x2-y2
=(x+y)(x-y)
=($\sqrt{2}+1+\sqrt{2}-1$)($\sqrt{2}+1-\sqrt{2}+1$)
=$2\sqrt{2}$×2
=4$\sqrt{2}$;
(2)x2+2xy+y2
=(x+y)2
=($\sqrt{2}+1+\sqrt{2}-1$)2
=(2$\sqrt{2}$)2
=8.
点评 本题考查二次根式化简求值,解题的关键是明确二次根式化简求值的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.与-3x2y是同类项的是( )
| A. | -2x2y | B. | -3xy2 | C. | 2x3y | D. | 5xy |

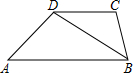 如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.
如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.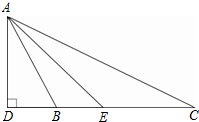 如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.
如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.