题目内容
5.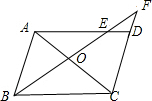 如图,平行四边形ABCD中,过B点作直线交AC、AD于O、E,交CD的延长线于F点,
如图,平行四边形ABCD中,过B点作直线交AC、AD于O、E,交CD的延长线于F点,(1)求证:OB2=OE•OF
(2)若AB=4,BC=6,DF=2,求AE的长.
分析 (1)由AB∥CD得到△AOB∽△COE,于是得到OE:OB=OC:OA,根据AD∥BC于是得到△AOF∽△COB,推出OB:OF=OC:OA,进而得出OB2=OF•OE;
(2)由平行四边形的性质:对边平行易证△ABE∽△DFE,再由相似三角形的性质:对应边的比值相等即可求出AE的长.
解答 解:
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△AOB∽△COE.
∴OE:OB=OC:OA;
∵AD∥BC,
∴△AOF∽△COB.
∴OB:OF=OC:OA.
∴OB:OF=OE:OB,
即OB2=OF•OE;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=6,
∴△ABE∽△DFE,
∴DF:AB=DE:AE,
∵AB=4,DF=2,
∴2:4=(6-AE):AE,
解得:AE=4.
点评 此题考查了相似三角形的判定和性质,综合性较强,有一定难度,证线段的乘积相等,通常转化为比例式形式,再证明所在的三角形相似,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
17.小明饶着一个五边形的花圃走了一圈,他一共转了多少度( )
| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
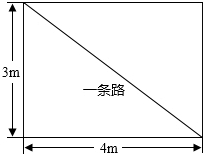 在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
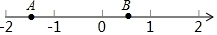 如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示-1$\frac{1}{2}$,设点B所表示的数为m
如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示-1$\frac{1}{2}$,设点B所表示的数为m