题目内容
13.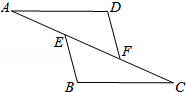 如图,已知点E,F在AC上,AD∥BC,DF=BE,添加的一个条件(不要在图中增加任何字母和线),使△ADF≌△CBE.你添加的条件是:∠D=∠B.
如图,已知点E,F在AC上,AD∥BC,DF=BE,添加的一个条件(不要在图中增加任何字母和线),使△ADF≌△CBE.你添加的条件是:∠D=∠B.证明:
分析 添加条件∠D=∠B,首先根据AD∥BC可得∠A=∠C,再加上条件DF=BE可以用AAS证明三角形全等.
解答 解:添加条件∠D=∠B,
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,$\left\{\begin{array}{l}{∠A=∠C}\\{∠D=∠B}\\{DF=EB}\end{array}\right.$,
∴△ADF≌△CBE(AAS).
故答案为:∠D=∠B.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
1.如果一个三角形有两边长分别是3和5,那么第三边长可能是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
3.点A、B分别是数-3、-$\frac{1}{2}$在数轴上对应的点,把线段AB沿数轴向右移动到A′B′,且线段A′B′的中点对应的数是3,则点A′对应的数是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1$\frac{3}{4}$ | D. | 4$\frac{1}{4}$ |
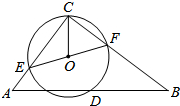 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,⊙O过C、D两点且分别交边AC、BC于点E、F,连接CO、EF.下列结论:
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB的中点,⊙O过C、D两点且分别交边AC、BC于点E、F,连接CO、EF.下列结论: