题目内容
11.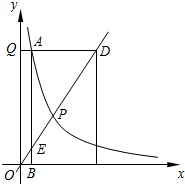 如图,已知正比例函数的图象与反比例函数的图象都经过点P(2,3),点D是正比例函数图象上的一点,过点D作y轴的垂线,垂足分别Q,DQ交反比例函数的图象于点A,过点A作x轴的垂线,垂足为B,AB交正比例函数的图于点E.
如图,已知正比例函数的图象与反比例函数的图象都经过点P(2,3),点D是正比例函数图象上的一点,过点D作y轴的垂线,垂足分别Q,DQ交反比例函数的图象于点A,过点A作x轴的垂线,垂足为B,AB交正比例函数的图于点E.(1)求正比例函数解析式、反比例函数解析式.
(2)当点D的纵坐标为9时,求:点E的坐标.
分析 (1)根据待定系数法求得即可;
(2)把y=9代入反比例函数的解析式即可求得A的坐标,把A点的横坐标代入正比例函数的解析式即可求得E的坐标.
解答 解:(1)设正比例函数解析式为y=mx,反比例函数解析式y=$\frac{k}{x}$(m≠0,k≠0),
把P(2,3)代入y=mx得3=2m,解得m=$\frac{3}{2}$,
∴正比例函数解析式为y=$\frac{3}{2}$x,
把P(2,3)代入y=$\frac{k}{x}$得,3=$\frac{k}{2}$,解得k=6,
∴反比例函数解析式为y=$\frac{6}{x}$;
(2)把y=9代入y=$\frac{6}{x}$,得9=$\frac{6}{x}$,解得x=$\frac{2}{3}$,
∴A($\frac{2}{3}$,9),
把x=$\frac{2}{3}$代入y=$\frac{3}{2}$x,得y=$\frac{3}{2}$×$\frac{2}{3}$=1,
∴E($\frac{2}{3}$,1).
点评 本题考查了待定系数法求一次函数的解析式和反比例函数的解析式以及反比例函数和一次函数的交点,根据D的纵坐标求得A的坐标,进而即可求得E的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如果一个三角形有两边长分别是3和5,那么第三边长可能是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
19.反比例函数y=$\frac{k}{x}$的图象与函数y=2x的图象没有交点,若点(-2,y1)、(-1,y2)、(1,y3)在这个反比例函数y=$\frac{k}{x}$的图象上,则下列结论中正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
3.点A、B分别是数-3、-$\frac{1}{2}$在数轴上对应的点,把线段AB沿数轴向右移动到A′B′,且线段A′B′的中点对应的数是3,则点A′对应的数是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1$\frac{3}{4}$ | D. | 4$\frac{1}{4}$ |