题目内容
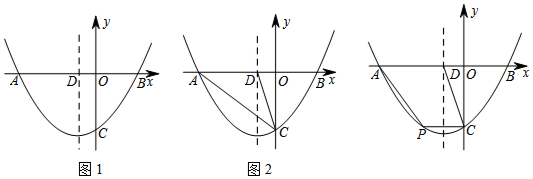
13. 如图在直角坐标系中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,如果点M在y轴右侧的抛物线上,S△AMO=$\frac{2}{3}$S△COB,那么点M的坐标是(1,-6)或(4,6).
如图在直角坐标系中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,如果点M在y轴右侧的抛物线上,S△AMO=$\frac{2}{3}$S△COB,那么点M的坐标是(1,-6)或(4,6).
分析 令y=0,解方程求出A,B两点,再令x=0,求出C点坐标,设出M点坐标,根据它在抛物线上和S△AMO=$\frac{2}{3}$S△COB,这两个条件求出M点坐标.
解答 解:∵y=x2-x-6为抛物线,
∵抛物线y=x2-x-6与x轴交于A,B两点,
令y=0,设方程x2-x-6=0的两根为x1,x2,
∴x1=-2,x2=3,
∴A(-2,0),B(3,0),
设M点坐标为(a,a2-a-6),(a>0)
∵S△AMO=$\frac{2}{3}$S△COB,
∴$\frac{1}{2}$×AO×|yM|=$\frac{2}{3}$×$\frac{1}{2}$×OC×|xB|,
∴$\frac{1}{2}$×2×|a2-a-6|=$\frac{2}{3}$×$\frac{1}{2}$×6×3,
解得,a1=0,a2=1,a3=-3,a4=4,
∵点M在y轴右侧的抛物线上,
∴a>0,
∴a=1,或a=4,
a2-a-6=12-1-6=-6,或a2-a-6=42-4-6=6
∴M点坐标为(1,-6)或(4,6).
故答案为:(1,-6)或(4,6).
点评 本题考查了一元二次方程与函数的关系,函数与x轴的交点的横坐标就是方程的根,若方程无根说明函数与x轴无交点,其图象在x轴上方或下方,两者互相转化,要充分运用这一点来解题,另外此题把三角形的面积关系式与函数的图象联系起来,计算量比较大,关键是利用三角形的几何关系来解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.2617与8213的大小关系是( )
| A. | 2617>8213 | B. | 2617=8213 | C. | 2617<8213 | D. | 不能判定 |
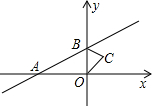 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).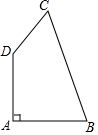 如图,在四边形ABCD中,DA⊥AB,DA=AB=$\sqrt{2}$,BC=$\sqrt{5}$,DC=1.则∠ADC的度数是135°.
如图,在四边形ABCD中,DA⊥AB,DA=AB=$\sqrt{2}$,BC=$\sqrt{5}$,DC=1.则∠ADC的度数是135°.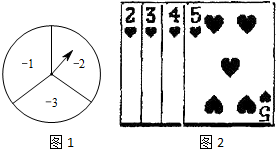 图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.
图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.