题目内容
10.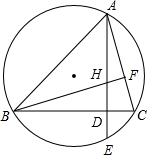 如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.
如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.(1)求证:DH=DE;
(2)若∠EAC=30°,求证:⊙O的半径R=EC.
分析 (1)连结CE,如图,利用等角的余角相得到∠1=∠3,再根据圆周角定理得到∠2=∠3,则∠1=∠2,加上CD⊥HE,则可判断△CEH为等腰三角形,然后根据等腰三角形的性质得HD=DE;
(2)连接OE,OC,根据圆周角定理和圆的性质即可得到结论.
解答 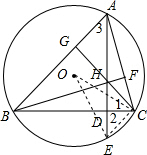 (1)证明:连结CE,连接CH并延长交AB于G,如图,
(1)证明:连结CE,连接CH并延长交AB于G,如图,
∵AD和BF为△ABC的高,
∴CG⊥AB,
∴∠1+∠B=90°,∠3+∠B=90°,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
而CD⊥HE,
∴△CEH为等腰三角形,
∴HD=DE;
(2)解:连接OE,OC,
∵∠EAC=30°,
∴∠COE=60°,
∵OC=OE,
∴△OCE是等边三角形,
∴⊙O的半径R=EC.
点评 本题考查了相似三角形的判定和性质,圆周角定理,等腰三角形的判定和性质,等边三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
已知用40元购进螺丝的数量与用16元购进螺母的数量相同.
(1)求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,要求两种配件的总量不超过3000个,且螺母的数量不少于500个.
①设购进螺丝x个,求x的取值范围;
②该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?
 某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:| 原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
| 螺丝 | a | 1.0 | 2.0 |
| 螺母 | a-0.3 | 0.6 |
(1)求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,要求两种配件的总量不超过3000个,且螺母的数量不少于500个.
①设购进螺丝x个,求x的取值范围;
②该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?
20. 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
(1)本次调查的样本容量为200;在频数分布表中,a的值为60,b的值为0.05,并将频数分布直方图补充完整;
(2)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%;
(3)根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%;
(3)根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.
小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.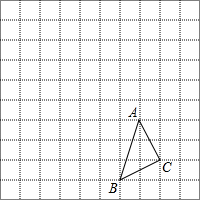 △ABC在方格中的位置如图所示.
△ABC在方格中的位置如图所示.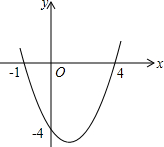 二次函数y=ax2+bx+c的图象如图所示,求:
二次函数y=ax2+bx+c的图象如图所示,求: 如图,M是弦AB(非直径)的中点,弦CD与弦AB相交于点M.当DC是⊙O直径时,CD⊥AB(只需填一个符合要求的答案).
如图,M是弦AB(非直径)的中点,弦CD与弦AB相交于点M.当DC是⊙O直径时,CD⊥AB(只需填一个符合要求的答案).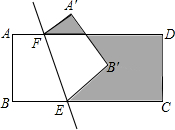 如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.
如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm. 如图,已知△ABC为等腰直角三角形,D是斜边BC上一点,连接AD,将AD绕点A顺时针旋转90°到AE处,过E作EF∥BC交AB于F,连接DE.CF,请判断四边形CDEF的形状,并说明理由.
如图,已知△ABC为等腰直角三角形,D是斜边BC上一点,连接AD,将AD绕点A顺时针旋转90°到AE处,过E作EF∥BC交AB于F,连接DE.CF,请判断四边形CDEF的形状,并说明理由.