题目内容
19. 如图,已知△ABC为等腰直角三角形,D是斜边BC上一点,连接AD,将AD绕点A顺时针旋转90°到AE处,过E作EF∥BC交AB于F,连接DE.CF,请判断四边形CDEF的形状,并说明理由.
如图,已知△ABC为等腰直角三角形,D是斜边BC上一点,连接AD,将AD绕点A顺时针旋转90°到AE处,过E作EF∥BC交AB于F,连接DE.CF,请判断四边形CDEF的形状,并说明理由.
分析 连结BE,如图,根据等腰直角三角形的性质得∠BAC=90°,∠ABC=∠ACB=45°,AB=AC,再根据旋转的性质得AE=AD,∠EAD=90°,则利用等角的余角相等得到∠EAB=∠DAC,于是根据旋转的定义,把△ADC绕点A顺时针旋转90°得到△AEB,则根据旋转的性质得BE=DC,∠ABE=∠ACD=45°,再利用EF∥BC得到∠EFB=∠ABC=45°,于是可判断△BEF为等腰直角三角形,则EF=EB,DE>BE,所以EF=CD,然后根据平行四边形的判定方法即可判断四边形CDEF为平行四边形.
解答 解:四边形CDEF为平行四边形.理由如下:
连结BE,如图,
∵△ABC为等腰直角三角形,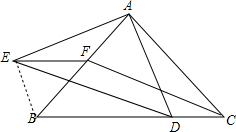
∴∠BAC=90°,∠ABC=∠ACB=45°,AB=AC,
∵AD绕点A顺时针旋转90°到AE处,
∴AE=AD,∠EAD=90°,
∴∠EAB=∠DAC,
∴△ADC绕点A顺时针旋转90°得到△AEB,
∴BE=DC,∠ABE=∠ACD=45°,
∵EF∥BC,
∴∠EFB=∠ABC=45°,
∴△BEF为等腰直角三角形,
∴EF=EB,DE>BE,
∴EF=CD,
而EF∥CD,
∴四边形CDEF为平行四边形.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和平行四边形的判定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
 如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.
如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.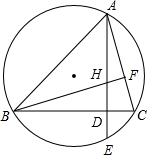 如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.
如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E. 如图,将左方的盒子展开成为一个十字型图形,它是下图中的( )
如图,将左方的盒子展开成为一个十字型图形,它是下图中的( )



 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且DE=6cm,则CD=6cm.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且DE=6cm,则CD=6cm. 如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:OB=OE.
如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:OB=OE. 如图,△ABC是等边三角形,过点C作CD⊥CB交∠CBA的外角平分线于点D,连结AD,过点C作∠BCE=∠BAD交AB的延长线于点E.
如图,△ABC是等边三角形,过点C作CD⊥CB交∠CBA的外角平分线于点D,连结AD,过点C作∠BCE=∠BAD交AB的延长线于点E.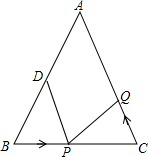 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.