题目内容
4．已知A（1，y1），B（2，y2）两点在反比例函数y=$\frac{5+2m}{x}$图象上，若y1＜y2，则实数m的取值范围是（ ）| A． | m＞0 | B． | m＜0 | C． | m$＞-\frac{5}{2}$ | D． | m$＜-\frac{5}{2}$ |
分析 根据已知和反比例函数的性质得出5+2m＜0，求出即可．
解答 解：∵0＜1＜2，A（1，y1），B（2，y2）两点在反比例函数y=$\frac{5+2m}{x}$图象上，y1＜y2，
∴5+2m＜0，
∴m＜-$\frac{5}{2}$，
故选D．
点评 本题考查了反比例函数图象上点的坐标特征，反比例函数的性质的应用，注意：反比例函数y=$\frac{k}{x}$（k≠0，k为常数），当k＞0时，在每个象限内，y随x的增大而减小，当k＜0时，在每个象限内，y随x的增大而增大．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15．
如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=12，则HE等于（ ）
如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=12，则HE等于（ ）| A． | 24 | B． | 12 | C． | 6 | D． | 8 |
为预防“手足口病”，某学校对教室进行“药熏消毒”．消毒期间，室内每立方米空气中的含药量y（mg）与时间x（分钟）的函数关系如图所示．已知，药物燃烧阶段，y与x成正比例，燃完后y与x成反比例．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．当每立方米空气中含药量低于1.6mg时，对人体才能无毒害作用．那么从消毒开始，经过50分钟后教室内的空气才能达到安全要求．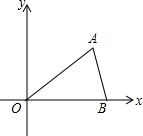
如图，在平面直角坐标系中，点A（$\sqrt{3}$，1）、B（2，0）、O（0，0），反比例函数y=$\frac{k}{x}$图象过点A．
如图，在平面直角坐标系中，△ABC是直角三角形，∠C=90°，AC∥x轴，A（-3，$\frac{3}{2}$），AC=2，BC=1．
16．下列点中，位于函数y=$\frac{2}{x}$图象上的是（ ）
| A． | （1，2） | B． | （1，$\frac{1}{2}$） | C． | （1，1） | D． | （2，$\frac{1}{2}$） |
如图，矩形ABCD被分成四部分．其中△CEF、△ABE、△ADF的面积分别是3、4、5，则△AEF的面积为8．
（1）计算：（2012-2016）0+$\root{3}{-8}$-（-$\frac{1}{3}$）-2．