题目内容
14. (1)计算:(2012-2016)0+$\root{3}{-8}$-(-$\frac{1}{3}$)-2.
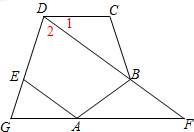
(1)计算:(2012-2016)0+$\root{3}{-8}$-(-$\frac{1}{3}$)-2.(2)如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G,求∠G的度数.
分析 (1)先分别用零指数幂,立方根,负指数化简,再计算即可;
(2)根据正五边形的内角及等腰三角形的性质计算即可.
解答 解:(1)原式=1-2-9=-10,
(2)∵ABCDE是正五边形,
∴∠C=∠CDE=108°CD=CB,
∴∠1=36°,
∴∠2=108°-36°=72°
∵AF∥CD,
∴∠F=∠1=36°,
∴∠G=180°-∠2-∠F=72°
点评 此题是多边形的内角和,主要考查了正五边形的内角的计算,等腰三角形的性质,解本题的关键是求出正五边形的内角.

练习册系列答案
相关题目
4.已知A(1,y1),B(2,y2)两点在反比例函数y=$\frac{5+2m}{x}$图象上,若y1<y2,则实数m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m$>-\frac{5}{2}$ | D. | m$<-\frac{5}{2}$ |
9.某林业部门要考察某种幼树在一定条件下的移植成活率,在同样的条件下对这种幼树进行大量移植,并统计成活情况,记录如下(其中频率结果保留小数点后三位)
由此可以估计幼树移植成活的概率为0.892.
| 移植总数(n) | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
| 成活数(m) | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
| 成活的频率$\frac{m}{n}$ | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
 某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为$\frac{5}{9}$.
某游戏的规则为:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.选手获得笔记本的概率为$\frac{5}{9}$.