题目内容
15．
如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=12，则HE等于（ ）| A． | 24 | B． | 12 | C． | 6 | D． | 8 |
分析 利用三角形中位线定理知DF=$\frac{1}{2}$AC；然后在直角三角形AHC中根据“直角三角形斜边上的中线等于斜边的一半”即可将所求线段EH与已知线段DF联系起来了．
解答 解：∵D、F分别是AB、BC的中点，
∴DF是△ABC的中位线，
∴DF=$\frac{1}{2}$AC（三角形中位线定理）；
又∵E是线段AC的中点，AH⊥BC，
∴EH=$\frac{1}{2}$AC，
∴EH=DF=12，
故选B．
点评 本题综合考查了三角形中位线定理、直角三角形斜边上的中线．三角形的中位线平行于第三边且等于第三边的一半．
练习册系列答案
相关题目
10．下列既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
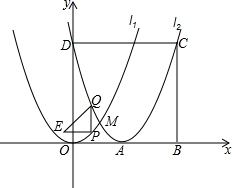如图，以A为顶点的抛物线l2是由抛物线l1：y=x2沿x轴向右平移2个单位后得到的，两抛物线相交于点M，抛物线l2与y轴交于点D，以OD为边向右作正方形ODCB，P为抛物线l1上一点，其横坐标为m（0≤m≤2），且点P不与点M重合，过点P作PQ∥y轴，交抛物线l2于点Q，将PQ绕点P逆时针旋转90°，得到线段PE，连结EQ．
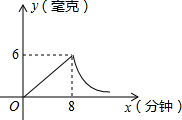为了预防流行性感冒，某学校对教室采用药熏消毒法进行消毒．已知药物燃烧时室内每立方米空气中的含药量y毫克）与时间x（分钟）成正比例；药物燃烧后，y与x成反比例（如图所示）．请根据图中提供的信息，解答下列问题：
4．已知A（1，y1），B（2，y2）两点在反比例函数y=$\frac{5+2m}{x}$图象上，若y1＜y2，则实数m的取值范围是（ ）
| A． | m＞0 | B． | m＜0 | C． | m$＞-\frac{5}{2}$ | D． | m$＜-\frac{5}{2}$ |