题目内容
19.计算:$|{-\sqrt{2}}|+{(\sqrt{3}-1)^0}+{(\frac{1}{2})^{-1}}-2cos{45°}$.分析 首先计算绝对值、零次幂、负整数指数幂、特殊角的三角函数值,然后再计算乘法,最后计算加减即可.
解答 解:原式=$\sqrt{2}$+1+2-2×$\frac{\sqrt{2}}{2}$,
=$\sqrt{2}$+3-$\sqrt{2}$,
=3.
点评 此题主要考查了实数的运算,解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
10.下列既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列交通标志中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.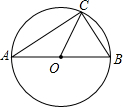 如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
 如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
4.已知A(1,y1),B(2,y2)两点在反比例函数y=$\frac{5+2m}{x}$图象上,若y1<y2,则实数m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m$>-\frac{5}{2}$ | D. | m$<-\frac{5}{2}$ |
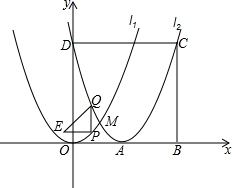 如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.
如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.