题目内容
16.下列点中,位于函数y=$\frac{2}{x}$图象上的是( )| A. | (1,2) | B. | (1,$\frac{1}{2}$) | C. | (1,1) | D. | (2,$\frac{1}{2}$) |
分析 把点的坐标代入函数解析式,看看左边和右边是否相等即可.
解答 解:A、把(1,2)代入y=$\frac{2}{x}$得:左边=右边,所以点(1,2)在函数y=$\frac{2}{x}$的图象上,故本选项正确;
B、把(1,$\frac{1}{2}$)代入y=$\frac{2}{x}$得:左边≠右边,所以点(1,$\frac{1}{2}$)不在函数y=$\frac{2}{x}$的图象上,故本选项错误;
C、把(1,1)代入y=$\frac{2}{x}$得:左边≠右边,所以点(1,1)不在函数y=$\frac{2}{x}$的图象上,故本选项错误;
D、把(2,$\frac{1}{2}$)代入y=$\frac{2}{x}$得:左边≠右边,所以点(2,$\frac{1}{2}$)不在函数y=$\frac{2}{x}$的图象上,故本选项错误;
故选A.
点评 本题考查了反比例函数图象上点的坐标特征的应用,能理解题意是解此题的关键.

练习册系列答案
相关题目
4.已知A(1,y1),B(2,y2)两点在反比例函数y=$\frac{5+2m}{x}$图象上,若y1<y2,则实数m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m$>-\frac{5}{2}$ | D. | m$<-\frac{5}{2}$ |
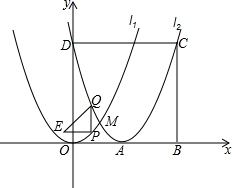 如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.
如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.
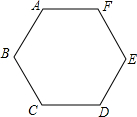 如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.
如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.